Introdução
A malária é uma doença evitável e curável; entretanto, no ano de 2018, ocorreram cerca de 228 milhões de casos da doença no mundo.1 A previsão oportuna de casos de malária permite a alocação de recursos adequados para o controle da doença e planejamento de sua eliminação.3 A iniciativa denominada ‘The Malaria Eradication Research Agenda’ analisou diversos aspectos importantes para a eliminação global da malária. A modelagem preditiva de casos foi sugerida como ferramenta de auxílio ao setor da Vigilância em Saúde, para o planejamento de ações de controle da infecção.4
Séries temporais mensais de novos casos podem ser estatisticamente ajustadas em funções matemáticas, utilizando-se de programas computacionais.6 A série temporal pode ser decomposta sob a ótica de três componentes básicas: (i) a componente sazonal, que representa o padrão cíclico da doença ao longo do tempo; (ii) a componente linear, entendida como uma tendência de aumento ou decréscimo linear da doença ao longo do tempo; e (iii) a componente estocástica, referente aos fatores intervenientes que afetam a série temporal sem padrão específico.
Modelos estatísticos de série temporal podem ser utilizados para a previsão de casos futuros. O modelo autorregressivo com média móvel integrada (ARIMA) é um método pioneiro para descrição e previsão de série temporal.9 O modelo de suavização exponencial (ETS) representa uma alternativa ao ARIMA.10 Modelos de suavização exponencial para ajustar padrões sazonais complexos (TBATS e BATS) são métodos considerados mais eficientes que o ARIMA.11 Outra alternativa encontra-se no modelo que divide a componente sazonal em subcomponentes (STLM).12
Os modelos descritos anteriormente são determinísticos e possuem estrutura estatística para decompor e ajustar as componentes sazonal e linear de série temporal; porém, não conseguem estimar a componente estocástica. Nesse sentido, foram propostas abordagens computacionais de aprendizado de máquina, para quantificar o efeito desta terceira componente: modelo estrutural (StructTS), modelo de redes neurais (NNETAR) e modelos com aprendizado de máquina (ELM, MLP) são exemplos dessas abordagens.9 Os modelos podem ser comparados com um modelo nulo, definido pelo valor constante da última observação.17
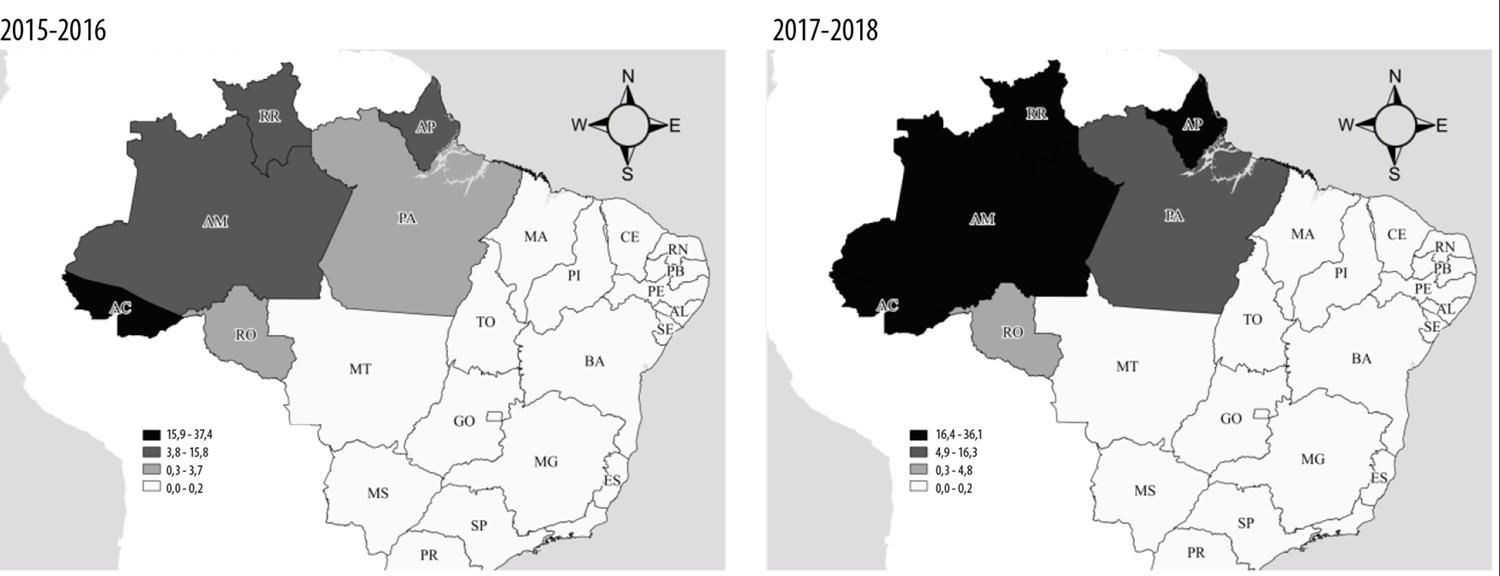
A premissa deste trabalho é a de que a vigilância em saúde pode utilizar modelos preditivos de série temporal, para prever o impacto da malária em determinado estado do Brasil. A incidência de casos de malária no estado do Amapá entre 2015 e 2018 foi, em média, de 17 casos por 1 mil habitantes, uma das maiores do país, ao lado das observadas para os estados do Acre (37/1 mil hab.), Amazonas (17/1 mil hab.) e Roraima (19/1 mil hab.) no mesmo período. É importante identificar a série temporal futura de casos de malária para o planejamento de medidas de controle. O presente estudo teve por objetivo avaliar a capacidade preditiva de diferentes modelos de série temporal dos casos de malária no estado do Amapá.
Métodos
Aplicou-se uma abordagem estatística e computacional direcionada ao serviço de saúde em nível estadual, complementar às atividades de controle da malária no Brasil como um todo, acorde com os termos pactuados junto à Organização Mundial da Saúde (OMS) para a eliminação da doença.2
Trata-se de estudo ecológico de séries temporais, utilizando o número de casos de malária registrados no estado do Amapá no período de 1997 a 2016.
O Amapá constitui uma das mais importantes regiões endêmicas da malária no Brasil (Figura 1). Seu clima predominante, segundo a classificação climática de Köppen-Geiger, é tropical de monção, ou seja, quente e bastante úmido, com índice de pluviosidade médio de 3.300mm anuais. A maior parte do território do estado (73%; 97.000km2) é coberta por vegetação nativa. Em 2019, a população amapaense somava 830 mil hab., distribuídos entre 16 municípios.
Os dados de malária (casos autóctones, identificados por microscopia em lâmina positiva para plasmódio – decorrente da técnica de gota espessa) foram obtidos a partir dos seguintes sistemas de informações da Secretaria de Vigilância em Saúde do Ministério da Saúde (SVS/MS): Sistema de Informação do Programa Nacional de Controle da Malária (Sismal), sobre o período 1997-2003; e Sistema de Informação de Vigilância Epidemiológica – Malária (SIVEP-Malária), sobre o período 2003-2016.
Foram utilizadas três variáveis quantitativas discretas, transformadas em logaritmo natural:18
número de casos mensais de malária, de janeiro de 1997 a dezembro de 2015 (a variável foi utilizada para ajustar os parâmetros dos modelos estatísticos);
valores estimados, de janeiro a dezembro de 2016 (variável de previsão, foi utilizada no teste de capacidade preditiva dos modelos estatísticos); e
número de casos mensais de malária, de janeiro a dezembro de 2016 (variável de teste, foi comparada com a variável de previsão).
A abordagem estatística utilizada baseou-se em modelos de séries temporais. O primeiro procedimento foi testar se a série temporal era ou não estacionária com o teste de Dikey-Fuller, aumentado ao nível de significância de 5%, sendo que a premissa de estacionariedade foi assumida no uso dos modelos estatísticos, descritos mais adiante.
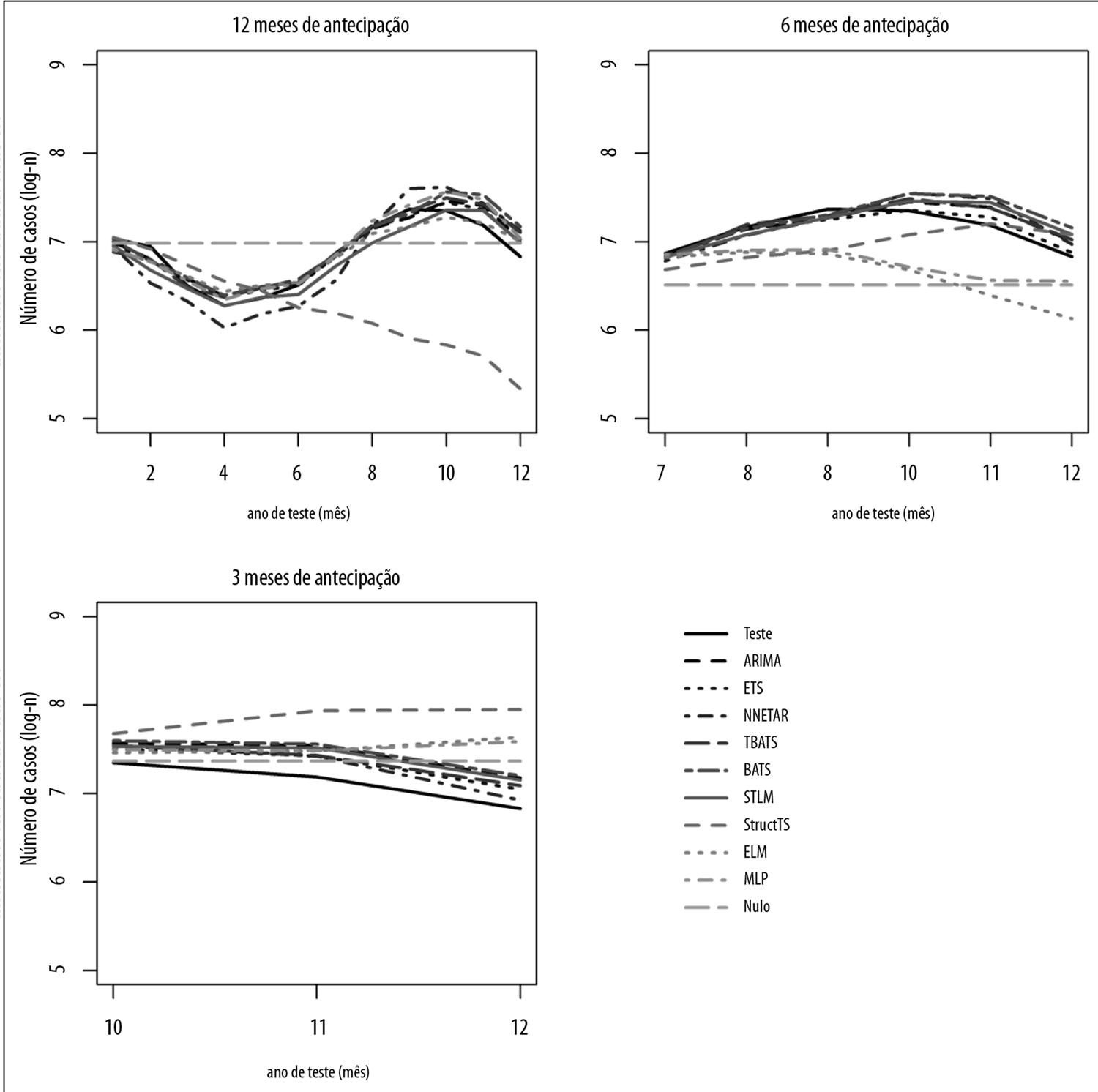
A série temporal abrangeu 240 meses, de janeiro de 1997 a dezembro de 2016, dividida em dois períodos: período de treino, de janeiro de 1997 a dezembro de 2015; e período de teste, de janeiro a dezembro de 2016. O número de casos mensais de malária no período de treino foi utilizado para ajustar cada um dos modelos estatísticos e estimar os parâmetros das componentes temporais (sazonalidade; tendência linear; efeito estocástico). O número de casos mensais de malária no período de teste foi utilizado para se comparar aos valores estimados pelos modelos estatísticos. O teste foi feito com três horizontes de tempo de previsão: 12 meses de antecipação (janeiro a dezembro de 2016); seis meses de antecipação (julho a dezembro de 2016); e três meses de antecipação (outubro a dezembro de 2016). O resultado de cada teste foi utilizado para avaliar a capacidade preditiva dos modelos.
Os modelos estatísticos utilizados foram:
Foram considerados três critérios para avaliação da capacidade preditiva dos modelos estatísticos:
Erro percentual absoluto médio (MAPE), em que At é o valor real e Ft é o valor da previsão. Os valores são somados para cada ponto previsto no tempo, e o resultado dividido pelo número de pontos n. Multiplicar por 100% torna o MAPE um erro de percentagem, de acordo com a seguinte fórmula:
Escala de MAPE relativo, em que o MAPE do modelo nulo é dividido pelos valores de MAPE dos demais modelos. Se o resultado dessa divisão é menor ou igual a 1, o modelo é classificado como ruim; se maior que 1 e menor ou igual a 2, o modelo é classificado como de baixa capacidade de previsão; e se é maior do que 2, o modelo apresenta capacidade de previsão confiável.
Coeficiente de incerteza (Theil’s U). Trata-se de uma medida de precisão relativa, que visa penalizar modelos estatísticos com desvios elevados em relação ao valor médio. Valores abaixo de 1 significam que a capacidade preditiva é confiável.17
Uma capacidade preditiva considerada aceitável, portanto, foi definida por (i) menor valor de MAPE, (ii) valores superiores a 2 para a escala MAPE do modelo nulo e (iii) valores abaixo de 1 para Theil’s U.
As análises foram realizadas no ambiente computacional R, mediante um script de programação corrigido e validado (Material suplementar), possível de ser reproduzido pelas equipes de vigilância dos municípios e estados do país.19
Resultados
O total de número de casos de malária foi de 403.832, a média, de 1.771 casos por mês, e mediana, de 1.518 casos/mês, com o primeiro quartil de 1.021 casos e o terceiro quartil de 2.079 casos – desvio-padrão (DP) = 918 casos. O valor do teste de Dikey-Fuller aumentado mostrou que a série temporal é estacionária (valor do teste = -5,352; p-valor <0,01). O número de casos mínimo foi de 487 (maio de 2014), enquanto o máximo foi de 5.944 (outubro de 2000), consistentemente com a natureza sazonal da malária no estado (Tabela 1).
Tabela 1 – Número de casos de malária confirmados por mês e ano, Amapá, janeiro de 1997 a dezembro de 2016
| Ano | Janeiro | Fevereiro | Março | Abril | Maio | Junho | Julho | Agosto | Setembro | Outubro | Novembro | Dezembro | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997 | 1.997 | 1.520 | 1.023 | 1.096 | 1.030 | 1.364 | 2.108 | 2.708 | 3.506 | 3.592 | 2.814 | 2.110 | 24.868 |
| 1998 | 1.633 | 1.863 | 1.566 | 1.524 | 1.773 | 1.899 | 2.005 | 2.534 | 3.001 | 1.795 | 1.929 | 1.047 | 22.569 |
| 1999 | 1.077 | 1.124 | 994 | 661 | 809 | 801 | 1.594 | 3.472 | 4.435 | 4.963 | 5.570 | 3.146 | 28.646 |
| 2000 | 2.473 | 2.731 | 1.632 | 1.269 | 1.563 | 1.714 | 2.377 | 4.336 | 3.767 | 5.944 | 4.574 | 2.898 | 35.278 |
| 2001 | 2.861 | 2.510 | 2.019 | 1.513 | 1.638 | 1.760 | 1.920 | 2.496 | 2.466 | 2.588 | 1.731 | 985 | 24.487 |
| 2002 | 1.422 | 1.250 | 849 | 671 | 593 | 649 | 971 | 1.953 | 2.330 | 2.174 | 2.144 | 1.251 | 16.257 |
| 2003 | 963 | 854 | 704 | 690 | 755 | 953 | 1.622 | 1.601 | 2.118 | 2.456 | 2.258 | 1.677 | 16.651 |
| 2004 | 1.949 | 1.972 | 1.453 | 987 | 1.014 | 1.126 | 1.408 | 1.954 | 1.848 | 2.731 | 2.387 | 1.841 | 20.670 |
| 2005 | 1.872 | 2.524 | 2.214 | 1.331 | 1.517 | 1.546 | 2.252 | 3.133 | 3.416 | 3.615 | 2.681 | 1.958 | 28.059 |
| 2006 | 2.505 | 1.500 | 1.231 | 1.101 | 1.582 | 1.637 | 2.403 | 3.393 | 3.431 | 4.371 | 3.750 | 2.386 | 29.290 |
| 2007 | 2.527 | 1.743 | 1.560 | 1.314 | 1.254 | 1.241 | 1.801 | 2.147 | 2.036 | 3.119 | 1.914 | 1.319 | 21.975 |
| 2008 | 1.217 | 957 | 823 | 770 | 872 | 745 | 960 | 1.121 | 1.721 | 2.099 | 2.144 | 1.702 | 15.131 |
| 2009 | 1.558 | 1.133 | 955 | 860 | 1.049 | 1.036 | 1.096 | 1.501 | 1.816 | 1.783 | 1.541 | 1.176 | 15.504 |
| 2010 | 1.466 | 1.143 | 994 | 730 | 892 | 970 | 1.384 | 1.390 | 1.292 | 1.553 | 2.072 | 1.502 | 15.388 |
| 2011 | 1.119 | 872 | 830 | 723 | 923 | 941 | 1.348 | 2.254 | 2.324 | 2.639 | 3.115 | 1.910 | 18.998 |
| 2012 | 1.685 | 1.257 | 1.040 | 693 | 863 | 917 | 1.272 | 1.344 | 1.234 | 1.619 | 1.925 | 1.432 | 15.281 |
| 2013 | 1.675 | 1.401 | 939 | 842 | 710 | 717 | 918 | 1.272 | 1.445 | 2.121 | 2.004 | 1.250 | 15.294 |
| 2014 | 1.057 | 806 | 599 | 516 | 487 | 516 | 646 | 1.201 | 1.844 | 2.163 | 2.199 | 1.521 | 13.555 |
| 2015 | 1.504 | 1.097 | 767 | 597 | 558 | 635 | 971 | 1.234 | 1.705 | 1.906 | 1.606 | 1.078 | 13.658 |
| 2016 | 1.138 | 1.040 | 667 | 532 | 580 | 673 | 962 | 1.296 | 1.585 | 1.554 | 1.321 | 925 | 12.273 |
Na Tabela 2, são apresentadas as performances dos modelos de acordo com os critérios de avaliação da capacidade preditiva e os três horizontes de tempo de previsão selecionados. Nos horizontes de 12 e seis meses de antecipação, todos os modelos determinísticos (ETS, ARIMA, STLM, BATS e TBATS) mostraram capacidade preditiva confiável. Entretanto, nenhum dos modelos estocásticos apresentou confiabilidade na previsão de casos futuros de malária nesses horizontes de antecipação.
Tabela 2 – Comparação de desempenho de modelos estatísticos em acordo com os critérios de avaliação de modelos e os tempos de previsão de cada horizonte de antecipação para os casos mensais de malária do Amapá
| Tempo de previsão no horizonte de antecipação de 12 meses | Tempo de previsão no horizonte de antecipação de 6 meses | Tempo de previsão no horizonte de antecipação de 3 meses | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Modelos | MAPEa | Escala de MAPEa relativo | Theil’s U | Modelos | MAPEa | Escala de MAPEa relativo | Theil’s U | Modelos | MAPEa | Escala de MAPEa relativo | Theil’s U |
| ETS | 1,25 | 3,76 | 0,40 | ETS | 0,76 | 11,28 | 0,29 | NNETAR | 2,47 | 1,44 | 0,64 |
| ARIMA | 1,39 | 3,38 | 0,47 | ARIMA | 1,47 | 5,83 | 0,56 | ETS | 2,87 | 1,24 | 0,82 |
| TBATS | 1,57 | 2,99 | 0,52 | TBATS | 1,60 | 5,36 | 0,58 | TBATS | 3,28 | 1,09 | 0,91 |
| ELM | 1,64 | 2,87 | 0,50 | STLM | 1,99 | 4,31 | 0,73 | Nulo | 3,56 | 1,00 | 1,45 |
| STLM | 1,63 | 2,88 | 0,57 | NNETAR | 2,16 | 3,97 | 0,76 | STLM | 3,96 | 0,90 | 1,17 |
| MLP | 1,66 | 2,83 | 0,55 | BATS | 2,24 | 3,83 | 0,93 | ARIMA | 4,36 | 0,82 | 1,27 |
| BATS | 1,81 | 2,60 | 0,68 | StructTS | 3,57 | 2,40 | 1,29 | BATS | 4,67 | 0,76 | 1,34 |
| NNETAR | 3,29 | 1,43 | 1,01 | MLP | 5,24 | 1,64 | 1,96 | MLP | 5,74 | 0,62 | 2,08 |
| Nulo | 4,70 | 1,00 | 1,63 | ELM | 6,97 | 1,23 | 2,53 | ELM | 5,82 | 0,61 | 2,20 |
| StructTS | 10,15 | 0,46 | 3,75 | Nulo | 8,57 | 1,00 | 2,88 | StructTS | 10,44 | 0,34 | 3,43 |
a) MAPE: erro percentual absoluto médio.
Notas:
ARIMA, ETS, TBATS, BATS e STLM: modelos determinísticos.
StructTS, NNETAR, ELM e MLP: modelos estocásticos.
Nulo: modelo nulo.
Surpreendentemente, o horizonte de três meses de antecipação se mostrou desafiador para todos os modelos. Afinal, nenhum modelo foi considerado confiável para a realização de previsão de casos de malária com três meses de antecipação (Figura 2).
Discussão
Os modelos determinísticos mostraram-se confiáveis para a previsão de número de casos mensais de malária nos próximos 12 ou seis meses de antecipação, no estado do Amapá. Um resultado que pode ser interpretado da seguinte forma: a série temporal em estudo possui características que possibilitaram o melhor desempenho dos modelos determinísticos, isto porque séries temporais com (i) forte componente sazonal, (ii) relativamente baixa tendência linear (i.e., estacionariedade temporal) e (iii) efeito estocástico pequeno ou nulo são ajustadas satisfatoriamente, por modelos determinísticos, a exemplo do ARIMA. Os modelos estatísticos com capacidade de detecção de efeitos estocásticos podem, teoricamente, apresentar melhor desempenho, comparados aos determinísticos, no caso de séries temporais com (i) ausência de sazonalidade, (ii) alta tendência linear e (iii) efeitos estocásticos presentes.20 Entretanto, nenhum dos modelos avaliados apresentou resultados confiáveis para a antecipação de número de casos mensais de malária no horizonte de três meses. A previsão de malária em períodos futuros curtos também resultou insatisfatória para outro estudo, no qual foram aplicados modelos determinísticos em distritos do Sri Lanka, entre 1972 e 2005.18 Aquele estudo desencorajou o uso de modelos estatísticos destinados à previsão de casos de malária em período proximal futuro de um mês de antecedência, não obstante o prazo do estudo do Sri Lanka ser ainda mais curto que o menor prazo estimado aqui.
Uma limitação da abordagem do trabalho em tela encontra-se na impossibilidade de previsão de casos de malária em períodos curtos de antecedência, como o de 3 meses. Outra limitação reside no fato de, ao utilizar o estado do Amapá como unidade de análise, informações na escala local serem perdidas. As vantagens da presente abordagem, entretanto, estão na possibilidade de previsão de casos de malária com 12 ou seis meses de antecipação e no uso de modelos estatísticos determinísticos. Estes modelos, de melhor entendimento para os gestores, tornam mais viável a implementação dessa ferramenta nos serviços de saúde.21
O uso potencial de técnicas de séries temporais em estudos epidemiológicos, vigilância de doenças e previsão de surtos para malária tem sido explorado em diversos trabalhos.18 Por exemplo, um estudo com delineamento similar, realizado no norte da Tailândia no período de 1999 a 2004, encontrou que modelos determinísticos permitem previsão futura de malária e dengue com antecipação de um a quatro meses, a ponto de seus autores sugerirem o uso desses modelos para a alocação de recursos no controle e prevenção dessas doenças.22 Outro estudo com modelos determinísticos, realizado no Sudão, de 2009 a 2013, evidenciou que a capacidade preditiva dos modelos utilizados variou de acordo com cada estado (daquele país).23 Modelos determinísticos utilizados para a previsão de malária no Afeganistão, entre 2005 e 2015, resultaram em previsões confiáveis para horizontes de 12 até quatro meses de antecipação.24
Considerando-se que, entre os modelos determinísticos, o ARIMA se apresenta como o mais aplicado na literatura e possui característica de previsão para doenças afetadas pela sazonalidade,22recomenda-se sua implementação como protocolo de previsão de casos mensais de malária em horizontes de longo prazo – 12 ou seis meses – na escala do estado da Amazônia brasileira.










 texto en
texto en