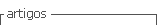Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Epidemiologia e Serviços de Saúde
versão impressa ISSN 1679-4974versão On-line ISSN 2237-9622
Epidemiol. Serv. Saúde v.13 n.3 Brasília set. 2004
http://dx.doi.org/10.5123/S1679-49742004000300003
Metodologia de correção e ajuste da mortalidade com tábuas-modelo de vida atualizadas para o Brasil*
Correction and adjustment method for mortality with updated life table model for Brazil
Paulo Campanário; Paulo Borlina Maia
Fundação Seade – Sistema Estadual de Análise de Dados, São Paulo-SP
RESUMO
O objetivo deste trabalho foi gerar um sistema ou modelo de tábuas de vida atualizado, específico para o Brasil, com o intuito de obter dados de mortalidade por sexo e idade das microrregiões e dos municípios que apresentam registro civil incompleto. O modelo foi construído a partir de variáveis que mantêm elevadas correlações com a mortalidade infantil das microrregiões do país. Criou-se, para cada uma dessas microrregiões, um índice similar ao Índice de Desenvolvimento Humano (IDH) da Organização das Nações Unidas (ONU), de tal forma que cada uma delas passou a possuir índices, dos quais resultou uma média e um índice geral de correlação com a mortalidade infantil bastante elevado. O ordenamento dessas microrregiões tendo por referência os respectivos índices possibilitou a criação de 40 macrorregiões, cada uma delas com, pelo menos, um milhão de habitantes, base estatística para a criação do modelo aqui proposto. A aplicação do modelo a partir das informações de mortalidade infantil estimadas pela Fundação Instituto Brasileiro de Geografia e Estatística (IBGE) mostrou-se satisfatória. Além da mortalidade infantil, outros pontos de partida poderão ser utilizados, como dados censitários sobre orfandade, viuvez, etc.
Palavras-chaves: tábua de vida; mortalidade; modelo; Brasil.
SUMMARY
The objective of this study was to generate a system or model of life tables, updated and specific for Brazil, to obtain mortality data by sex and age for the micro-regions and municipal districts with incomplete civil registration. The model was built from variables that are highly correlated with the infant mortality in the micro-regions. An individual index, similar to the Human Development Index (HDI) used by the United Nations‘s (UN), was created for each microregion; the average of these indexes represents a general index, which has a high correlation with infant mortalty. The ordering of these micro-regions based on their respective indexes permitted 40 macro-regions with at least one million inhabitants to be created. This is the statistical basis for the present model that was created. The application of this model, using infant mortality information estimated by the Brazilian Institute of Geography and Statistics Foundation (IBGE), was satisfactory. Besides infant mortality, the model might be applied to other data, such as census data on orphanhood, widowhood, etc.
Key words: life table; mortality; model; Brazil.
Introdução
Este artigo origina-se do projeto "Desenvolvimento de Metodologias Alternativas para a Análise de Bancos de Dados Secundários",1 demandado pelo então Centro Nacional de Epidemiologia (Cenepi), da Fundação Nacional de Saúde (Funasa) – atual Secretaria de Vigilância em Saúde (SVS), do Ministério da Saúde –, no âmbito do Projeto Vigisus, cujo relatório final foi entregue em agosto de 2001. O seu objetivo foi apresentar técnicas para o uso de parte do banco de dados do sistema de vigilância epidemiológica. O relatório foi estruturado em dois grandes capítulos. O Capítulo I apresentou a metodologia de uso de análise fatorial e de clusters para a preparação de um banco de dados resumido, para facilitar a tomada de decisões em políticas públicas de saúde. O Capítulo II tratou de metodologia de correção e ajuste da mortalidade das microrregiões brasileiras com a utilização de novo modelo de tábuas de vida adaptado à situação atual do país. O presente artigo é um resumo desse segundo capítulo.
Deve-se enfatizar que as taxas de mortalidade têm enorme importância para fins epidemiológicos. Entretanto, constata-se, ainda hoje, uma omissão significativa dos dados fornecidos pelo registro civil na maioria dos Estados da Federação. Além do problema do sub-registro, centenas de Municípios cujas taxas de mortalidade não podem ser calculadas devido ao problema estatístico de sua pequena população, apresentam, conseqüentemente, um número excessivamente pequeno de óbitos anuais, causador de oscilações muito grandes nessas taxas.
Para minorar os problemas acima citados, a Fundação Instituto Brasileiro de Geografia e Estatística (IBGE), em 1980, propôs o trabalho "Brasil: Tábuas- Modelo de Mortalidade e Populações Estáveis", publicado em 1981.2 Nele, é apresentado um modelo de tábuas de mortalidade segundo diferentes níveis de esperança de vida ao nascer, adaptado aos perfis de mortalidade por sexo e idades prevalecentes no Brasil antes dos anos 80. Existem vários modelos similares, adaptados a diferentes regiões do mundo, como o "Regional Model Life Tables and Stable Populations",3 de Coale & Demeny, o "Model Life Tables for Under- Developed Countries",4 das Nações Unidas, o "Model Life Tables for Developing Dountries",5 mais recente e também das Nações Unidas, o "Nouvelles Tables-Type de Mortalité",6 de Lerdermann, etc.
A idéia essencial desses modelos, ainda válida, é a de que, a cada nível de mortalidade em geral (ou de esperança de vida ao nascer) corresponde uma forma específica de taxas de mortalidade por grupos de idades e sexo. Uma explicação detalhada dessa relação pode ser encontrada no citado trabalho de Coale & Demeny. Por outro lado, a partir dos anos 80, o Brasil passou por um processo de desenvolvimento que provocou certas modificações nos padrões de mortalidade. Pode-se citar, entre outras, a diminuição abrupta da mortalidade infantil em razão dos progressos ocorridos no saneamento básico, das campanhas de vacinação em massa, etc.; e um aumento da mortalidade, principalmente masculina e em jovens adultos, por violências. Essas e outras transformações fazem com que as curvas de mortalidade também se modifiquem, especialmente a partir dos anos 80.
Portanto, o problema da utilização desses modelos, especificamente o modelo do IBGE, é seu grau de atualização e não uma possível caducidade das hipóteses sobre as quais eles se fundamentam. O que se propõe, nesta oportunidade, é a construção de um novo modelo de mortalidade, atualizado a partir de dados do país – oriundos dos Estados, regiões ou Municípios – que tenham uma cobertura do registro civil superior a 95%, baseando-se em quantificações divulgadas nos "Indicadores de Dados Básicos para a Saúde no Brasil 2001"7 da Rede Interagencial de Informações para a Saúde (Ripsa), do Ministério da Saúde. Critério igual de cobertura de 95% pode ser encontrado em Vasconcelos.8
Por outro lado, o modelo aqui elaborado é considerado adequado para o período a partir dos anos 80, tão-somente. Com efeito, além de seus dados serem recentes, utilizou-se, inclusive como ponto de partida, o já citado modelo de tábuas de vida,2 cujos esclarecimentos estão disponíveis neste artigo. Fica implícito que este último modelo ainda é válido para a década de 70 e anteriores.
Metodologia
Correção e ajuste da mortalidade com sistema de tábuas-modelo de mortalidade atualizado
Nos diferentes bancos de dados eletrônicos à disposição, foram encontradas, aproximadamente, 400 variáveis. Muitas delas, com certeza, apresentariam qualidade deficiente. Outras, provavelmente, seriam redundantes. E outras, irrelevantes sob o ponto de vista social, econômico e/ou epidemiológico.
Como primeiro passo, o grupo de pesquisadores envolvidos no projeto consultou uma bibliografia específica sobre a qualidade e as características das informações disponíveis nos bancos de dados.9-14 A seguir, reuniu-se, diversas vezes, com pesquisadores que se dedicam a analisar esses bancos de dados (ver Agradecimentos, no final do artigo). Seguidamente, para filtrar tais variáveis e dar início ao Capítulo I do projeto, foi utilizada a Técnica de Delfos, desenvolvida pela Rand Corporation nos anos 60; para exemplo mais detalhado dessa técnica, ver Adams.15 Esse procedimento metodológico vem sendo utilizado amplamente, nos meios acadêmicos e empresariais, quando o assunto é complexo e não se dispõe de conhecimentos práticos para opções técnicas ou metodológicas, prognósticos, etc. Sua característica essencial é, dada uma pesquisa qualquer, a tomada de decisões pela maioria do grupo de técnicos envolvidos no trabalho, após discussões e confronto de idéias. No caso específico das 400 variáveis, um assunto de abordagem altamente complexa, os técnicos discutiram todas elas, uma a uma, trocaram idéias sobre as informações e conhecimentos adquiridos nos livros e reuniões especificados e decidiram, por maioria, quais seriam as mais relevantes para o estudo. Dessa forma, foram escolhidas 188. A partir destas, excluindo as que apresentavam altas proporções de informação ignorada, pequena variabilidade, grande número de Municípios ou microrregiões sem informação, etc., restaram 40. Finalmente, via procedimentos estatísticos, foram eliminadas as variáveis que forneciam informações similares (redundantes), chegando-se às 25 indicadas na relação abaixo, ponto de partida empírico dos Capítulos I e II do relatório do projeto que deu origem ao presente artigo.

A análise fatorial, realizada no Capítulo I do relatório do projeto, permitiu sintetizar a maior parte das informações contidas nessas 25 variáveis, em três indicadores ou fatores: um primeiro, essencialmente socioeconômico, caracterizado por dados de escolarização, finanças públicas e serviços de saúde especializados, principalmente de caráter ambulatorial; um segundo, que se pode interpretar como expressão da acessibilidade ao sistema hospitalar público [financiado pelo Sistema Único de Saúde (SUS)]; e um terceiro, em que se expõem as despesas com atividades sociais. A partir desses fatores, chegou-se a quatro clusters, úteis para a tomada de decisões em políticas públicas de saúde.
Por outro lado, para a elaboração da metodologia de correção e ajuste da mortalidade, ou seja, o Capítulo II do projeto e também objeto deste artigo, foi introduzida, como indicador geral de mortalidade, a taxa de mortalidade infantil corrigida, obtida em "Estimativas de Mortalidade Infantil por Microrregiões e Municípios"16 e adotada, oficialmente, pelo Ministério da Saúde. Trata-se da única informação confiável e disponível sobre mortalidade do país, para todas as suas microrregiões. Prováveis erros no cálculo dessa taxa – estimada por métodos indiretos – devem ser relativizados, pelo menos no que se refere ao seu aproveitamento nesta pesquisa. Em primeiro lugar porque, juntamente com outras variáveis, a referida taxa foi empregada para gerar agrupamentos de microrregiões com mais de um milhão de habitantes, de tal forma a se chegar a 40 macrorregiões que apresentam taxas de mortalidade em uma seqüência crescente, o que será justificado posteriormente. Por esse motivo, pequenos desvios, para mais ou para menos, praticamente não afetam esses aglomerados. Em segundo lugar, a taxa foi utilizada apenas para exemplificar uma das aplicações do modelo proposto, como se verá mais adiante.
As correlações entre as taxas de mortalidade infantil das microrregiões e os três fatores citados são baixas (fatores I, II e III com correlações, respectivamente, de -0,51, -0,33 e -0,26). Assim, esses fatores não puderam servir, como se esperava de início, de ponto de partida para se chegar ao modelo de mortalidade proposto. Isso significa, em termos práticos, que não se podem relacionar os clusters encontrados com a mortalidade.
Apesar de não poder utilizar tais clusters, a equipe se valeu dessas 25 variáveis selecionadas na primeira parte do projeto. Foram feitas correlações de cada uma dessas variáveis com a variável mortalidade infantil e os valores oscilaram entre -0,15 (taxa de atendimento em urgência/emergência) e -0,73 (número de anos de estudo do chefe do domicílio). De todas elas, 17 foram descartadas por apresentarem pequena ou nenhuma correlação com a mortalidade infantil. Optou-se pelo critério de que só seriam aceitas as correlações inferiores a -0,5 ou superiores a +0,5, baseado na premissa de que, normalmente, com variáveis sociais, são níveis de correlação empiricamente aceitáveis. Eis as sete variáveis selecionadas:
- escolaridade média do chefe (número de anos de estudo, pertencente ao fator 1);
- porcentagem de chefes de domicílio com mais de 12 anos de instrução (fator 1);
- número de matrículas no ensino médio por 100 habitantes entre 15 e 19 anos de idade (fator 1);
- número de docentes por 100 pessoas entre 15 e 19 anos de idade (fator 1);
- porcentagem de pessoas de mais de dez anos de idade ocupadas em empresas, por 100 habitantes (fator 1);
- taxa de internação por doenças do aparelho circulatório (fator 2); e
- receita orçamentária per capita (fator 3).
Destas sete – todas apresentando valores negativos –, quatro mantêm uma relação direta com educação, apesar de serem independentes entre si. Elas foram selecionadas tendo em vista critérios estatísticos, como já foi afirmado. As três variáveis restantes medem, de uma ou outra forma, o grau de desenvolvimento da microrregião. Com efeito, a porcentagem de pessoas de mais de dez anos de idade ocupadas em empresas mede a porcentagem de pessoas com carteira de trabalho assinada ou, mais concretamente, a porcentagem de pessoas no setor formal da economia; a taxa de internação por doenças do aparelho circulatório mede a sofisticação do sistema de atendimento; e, finalmente, a receita orçamentária per capita mede o poderio econômico da microrregião. Em suma, a mortalidade geral e, principalmente, a infantil dependem do grau de educação das pessoas e do desenvolvimento da microrregião.
Esses dois grupos de variáveis – as 25 utilizadas no Capítulo I do relatório para definir clusters e as sete utilizadas neste estudo – representam duas realidades diferentes, mas complementares. Por um lado, as primeiras e seus quatro agrupamentos indicam a morbidade das pessoas e a sua situação de saúde por microrregiões, podendo sinalizar políticas públicas específicas para aperfeiçoar o atendimento ambulatorial e a internação. Já as sete variáveis correlacionadas com a taxa de mortalidade infantil podem sinalizar políticas públicas específicas para diminuir a mortalidade, primordialmente infantil, ademais de serem úteis à criação das tábuas-modelo de mortalidade e seus inúmeros desdobramentos, caso das projeções populacionais, entre outros. Isso também significa que, nos dias de hoje, existe uma relativa autonomia entre morbidade, ou seja, o estado de saúde da população, e mortalidade. Contudo, é indiscutível que se deva almejar, sempre, a diminuição das duas, em prol do maior bem-estar social.
Pois bem: a partir das sete variáveis especificadas, criou-se, para cada uma delas, um índice que varia de 0 a 100, similar ao Índice de Desenvolvimento Humano (IDH) da Organização das Nações Unidas (ONU), tal como vem sendo definido e explicado, há anos, nos "Informes sobre Desarrollo Humano"17 do Programa das Nações Unidas para o Desenvolvimento (PNUD). Desse modo, cada microrregião passou a possuir sete índices, cuja média resultou em um índice geral, aqui denominado Índice de Variáveis Relacionadas com a Mortalidade, ou simplesmente IVRM. Sua correlação com a mortalidade infantil é igual a 0,73, bastante elevada para fins de análise social e epidemiológica.
No seguinte item, explica-se como foi utilizado o IVRM para se chegar às tábuas-modelo de mortalidade. Por ora, e apenas para efeitos de visualização, no mapa do Brasil, das microrregiões com seus respectivos índices, foi feita uma divisão do IVRM em dois grupos: um primeiro grupo de microrregiões com índices iguais ou inferiores a 30; e um segundo grupo com índices superiores a 30. Trata-se de uma divisão arbitrária, estabelecida depois de algumas tentativas de acerto e erro; no entanto, mostra um país conhecido de todos, dividido em dois, o que reforça a robustez metodológica do índice. Essas duas "grandes regiões", por assim dizer, são representadas no mapa da Figura 1: a primeira inclui a Região Norte, a Região Nordeste, o norte de Minas Gerais, o norte do Espírito Santo e, parcialmente, os Estados de Mato Grosso e Goiás; a segunda é formada pelos demais Estados da Região Centro-Oeste, todos os da Região Sul e os Estados de São Paulo, Rio de Janeiro e sul de Minas Gerais. As exceções são as capitais dos Estados dessa grande região constituída pelo Norte-Nordeste e mais alguns pontos (microrregiões) da outra "grande região", segundo o critério definido pelos pesquisadores.
Macrorregiões com cobertura de mortes aceitável
Para a criação de tábuas-modelo de mortalidade, necessita-se, em primeiro lugar, de dados de mortalidade confiáveis. Por esse motivo, foram utilizados somente os dados das microrregiões nos Estados com estatísticas de mortalidade cuja cobertura fosse superior a 95%. De acordo com fonte já indicada,7 somente o Rio Grande do Sul, o Paraná, Santa Catarina, São Paulo, Mato Grosso do Sul e o Rio de Janeiro fazem parte dessa categoria.
O passo seguinte foi separar as microrregiões pertencentes a esses Estados com cobertura elevada, das outras microrregiões. Restaram 185 microrregiões, de um total de 559, abarcando aproximadamente 40% da população do país.
Foi feita uma classificação dessas microrregiões segundo o IVRM, em ordem crescente. Depois, foram somadas as populações nessa mesma ordem, de forma a obter aglomerações de pelo menos um milhão de habitantes, número necessário à obtenção de curvas de mortalidade por sexo e idade, sem oscilações devidas a um reduzido número de mortes. Para maior segurança contra essas perturbações, foram utilizados dados de mortalidade disponíveis para os três anos mais recentes (1996, 1997 e 1998).
A microrregião do Rio de Janeiro, que abarca o Município do mesmo nome e alguns outros da sua Área Metropolitana, apresentou número bastante inferior de mortes no banco de dados do sistema de informações sobre mortalidade, se comparado com o número de mortes disponível na página eletrônica do Ministério da Saúde, possivelmente devido a algum erro na transmissão dos dados. O problema é que os dados do Ministério da Saúde, provavelmente corretos, não apresentam as mortes discriminadas por sexo e grupos etários, informação absolutamente necessária para gerar o modelo. Por esse motivo, foi descartada a microrregião do Rio de Janeiro. Chegou-se a um total de 40 macrorregiões classificadas segundo o IVRM e com pelo menos um milhão de habitantes.
Ao analisar o comportamento das probabilidades de morte por sexo e idades dessas 40 macrorregiões, observou-se que as curvas assim obtidas tinham padrões muito diferentes, sem relação com a ordem das macrorregiões no que diz respeito ao IVRM, fato que, aparentemente, invalidava a tentativa de criar um modelo de tábuas de mortalidade para o país. Contudo, depois de analisar diferentes possibilidades, constatou-se que tais padrões diferenciados apareciam, principalmente, no sexo masculino e em idades adultas jovens. A conclusão foi simples: as causas externas e a aids explicavam tais diferenças de padrão. Portanto, o passo seguinte foi eliminar as mortes por essas causas das restantes e gerar probabilidades de morte por idades sem esses fatores perturbadores. Sendo assim, o ponto de partida empírico das tábuas-modelo foi a mortalidade por sexo e idades sem causas externas e aids.
Metodologia para a criação de tábuas-modelo de mortalidade
O princípio básico que muitos pesquisadores adotaram para desenvolver tábuas-modelo de mortalidade é a relação estreita entre a esperança de vida ao nascer (ou aos 10 anos) e as probabilidades de morte em diferentes idades. Esse foi o princípio adotado nas tábuas-modelo já citadas.2-5 Normalmente, a relação é mais estreita: por um lado, entre a esperança de vida ao nascer e as probabilidades de morte dos menores de 1 ano, entre 1 e 4 e entre 5 e 9 anos; por outro lado, entre a esperança de vida aos 10 anos de idade e as probabilidades de morte dos grupos etários que seguem (acima dos 10 anos de idade).
Pode-se medir essa relação com correlações ou visualizá-la em um gráfico, onde o eixo x representa a esperança de vida ao nascer (ou aos 10 anos) e o eixo y representa as probabilidades de morrer de determinado grupo etário das 40 macrorregiões selecionadas (menores de 1 ano, 1 a 4, 5 a 9, etc.). No presente caso, foram realizados ensaios com as probabilidades e as esperanças de vida ao nascer e aos 10 anos. Concluiu-se que o modelo mais apropriado é o que relaciona a esperança de vida aos 10 anos com as probabilidades de morte em todas as idades.
O passo seguinte foi escolher a função mais apropriada para descrever a "nuvem" de pontos do gráfico da esperança de vida versus probabilidades de morte por idades. Foram tentadas inúmeras funções, a começar pelas utilizadas por Coale & Demeny e pelos autores do Modelo Brasil. Nenhuma delas se mostrou eficaz, pois não acompanhavam adequadamente a citada nuvem de pontos, o que se explica, talvez, pelo fato de o modelo pretendido apresentar características muito específicas. Em primeiro lugar, tenta-se gerar um modelo com dados recentes, referidos a 1997, localizado em um só ponto do tempo, ao contrário dos modelos já citados, que sempre abarcam um período de várias décadas. Em segundo lugar, as taxas futuras de qualquer região do Brasil não diminuirão com a mesma intensidade que a observada em décadas passadas, pois o país se encontra em estágio relativamente avançado de transição demográfica e epidemiológica, como concluem Figoli e Wong,18 Mello Jorge e Gotlieb,19 Barreto e Carmo.20
A função que melhor se adaptou às especificidades acima foi a logística, desde que aplicada com parâmetros apropriados, como será esclarecido a seguir. Essa função pode ser descrita como uma curva com um platô ou nível máximo (denominado assíntota superior), um mínimo (assíntota inferior) e uma transição contínua e suave entre esses dois extremos, com um ponto de inflexão entre eles. Uma boa descrição da função pode ser feita comparando-a ao perfil de um "tobogã". Essa função é definida por quatro parâmetros: a assíntota superior; a assíntota inferior; e dois pontos intermediários que definem a forma como a curva passa de uma assíntota a outra (mais ou menos inclinada, mais ou menos rapidamente, etc.). A curva logística e seus parâmetros são dados pelas fórmulas abaixo:
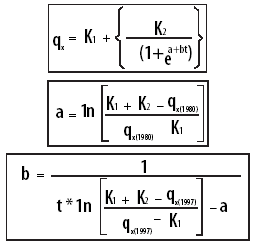
Na fórmula: qx é a probabilidade de morte na idade x; K1 é a assíntota inferior; K2 é a diferença entre a assíntota superior e a inferior; a e b são parâmetros; qx(1980) é a probabilidade média de morrer do Brasil na idade x em 1980 (a escolha deste ano específico será justificada mais adiante); qx(1997) é a probabilidade média de morrer do Brasil na idade x em 1997 (a escolha deste ano específico também será justificada mais adiante); e finalmente, t é uma escala definida a partir das esperanças de vida aos 10 anos de idade, cujo ponto zero corresponde a qx de 1980, o que, igualmente, será justificado mais adiante.
Como todas as taxas das macrorregiões são recentes (1996, 1997 e 1998, com média em 1997), pode-se assumir que, em um passado não tão remoto, elas tinham uma assíntota superior muito similar, haja vista o país ter passado rapidamente, a partir dos anos 50, pelas diferentes etapas da transição demográfica e epidemiológica. Pode-se, então, adotar a assíntota superior da função como um ponto do passado imediatamente anterior ao do início da transição demográfica, ou seja, nos anos 40, quando a mortalidade era relativamente homogênea e elevada. A esperança de vida ao nascer do Brasil, nessa década, era de aproximadamente 45 anos para homens e 50 para mulheres. Por esse motivo, adotou-se o Nível 11 das já citadas tábuas-modelo do IBGE 2 e suas respectivas probabilidades de morte por grupos etários. O Nível 11 apresenta, para mulheres, uma esperança de vida ao nascer de 50,1 anos e, para homens, de 44,6 anos. Ao adotar esse nível das tábuas-modelo do IBGE como assíntota superior, está-se assumindo, por conseguinte, que esse modelo – desenvolvido em 1981, com dados que iam de 1920 a 1970 –, serve como ponto de partida das probabilidades de morte mais elevadas no modelo aqui proposto. Como nosso objetivo é o de gerar um modelo representativo a partir dos anos 90, fica implícito que houve uma transição de padrão paulatina entre o modelo do IBGE e o aqui apresentado, ou, mais especificamente, entre os anos 40 e os anos 90.
A assíntota inferior foi definida como uma média dos quatro países que, nos dias de hoje, apresentam as menores taxas de mortalidade, ou seja, as maiores esperanças de vida ao nascer, e que tinham dados disponíveis sobre mortes por causas externas e aids. Foi excluído o Japão, cujas taxas, tão baixas, encontram-se demasiado distantes da nossa realidade para servir como um paradigma à mortalidade futura do Brasil. Os países selecionados foram o Canadá, os Estados Unidos da América, a França e a Alemanha. Foi feita uma média de suas probabilidades de morte por idades (sem causas externas e aids), sendo assim definida, para cada idade e sexo, uma probabilidade longínqua (futura) – a assíntota inferior.
Definidas as assíntotas superior e inferior, passou-se a buscar os dois pontos intermediários para que a curva (o "tobogã") assumisse uma forma adequada, ou seja, representasse a nuvem de pontos de 1997 da melhor maneira possível. Estatisticamente, a função logística definida a partir dos quatro parâmetros (assíntotas superior e inferior, e os dois pontos intermediários) deve ter uma correlação elevada com a nuvem de pontos de 1997, em cada grupo etário e para cada sexo.
Foram realizadas inúmeras tentativas até que fossem encontrados os dois pontos intermediários mais adequados. Tentou-se, para o primeiro deles, ou seja, o mais próximo da assíntota superior, adotar as probabilidades de morte da macrorregião com a maior probabilidade de morte; buscou-se, igualmente, calcular uma média das probabilidades das macrorregiões com as maiores mortalidades gerais; também tentou-se adotar as probabilidades de morte de vários pontos intermediários quaisquer entre os anos 50 e os 90, etc. A melhor solução foi adotar as probabilidades de morte por idades e sexo do Brasil em 1980 (cuja esperança de vida era de 64,8 anos para mulheres e de 59,9 anos para homens, localizada entre os níveis 17 e 18 do modelo do IBGE).
Tentativas análogas foram realizadas para encontrar o segundo ponto intermediário da função logística. O eleito foi a média das probabilidades de morte para cada idade e sexo, das macrorregiões, em 1997. Dessa forma, a função logística foi forçada a passar em meio à nuvem de pontos desse ano.
Em resumo, foram geradas 18 curvas logísticas para cada sexo (o número de grupos etários). As assíntotas superiores representam um ponto no passado, aproximadamente nos anos 40; as inferiores representam um ponto no futuro, para o qual foram utilizadas as médias das probabilidades de morte dos quatro países desenvolvidos selecionados. O primeiro ponto intermediário representa o país em 1980; e o outro ponto, o país em 1997.
Na Figura 2, pode-se visualizar como a função logística ajustou as probabilidades de morte por idades e sexo das macrorregiões. Todas as características dessa função podem ser conferidas na Tabela 1.
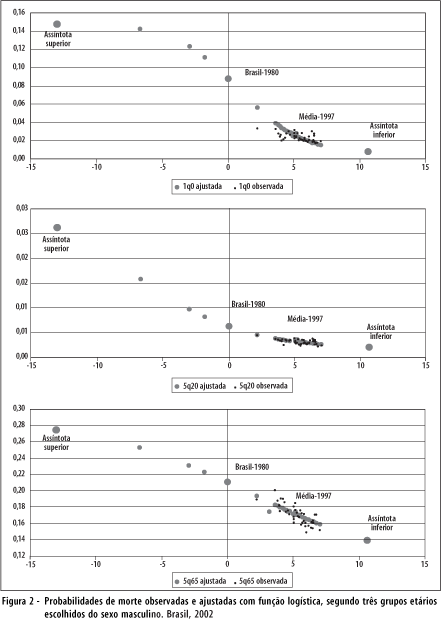
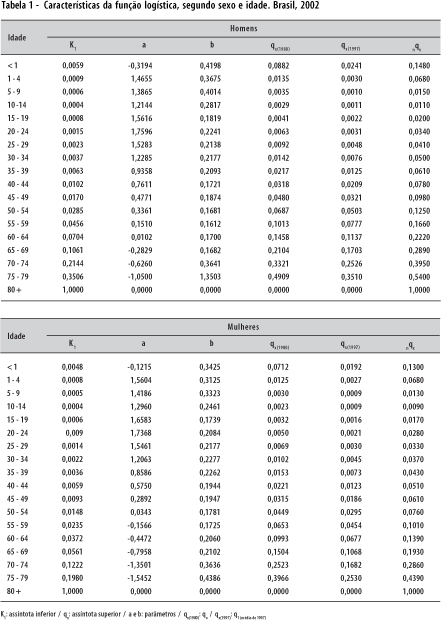
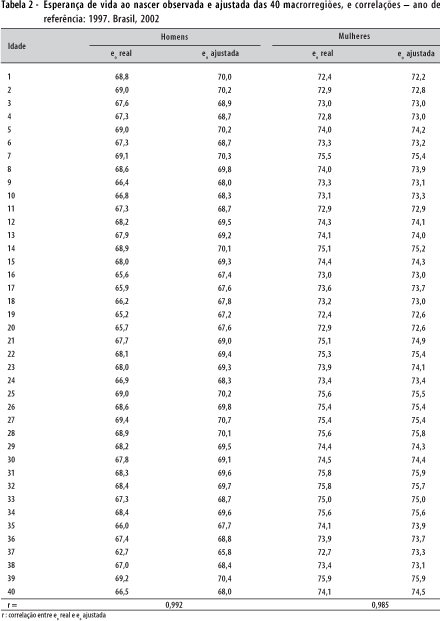
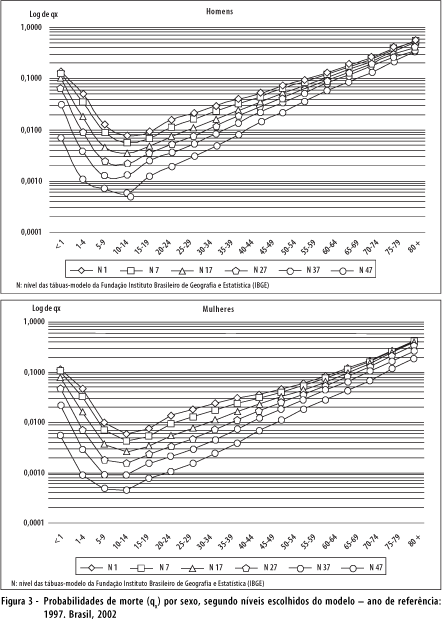
Os valores das esperanças de vida ao nascer observados e os ajustados com a função logística, das 40 macrorregiões, são muito similares (Tabela 2), sendo sua correlação bastante elevada: 0,992 e 0,985 para homens e mulheres, respectivamente. Esses fatos mostram que a função encontrada é robusta, o que justifica a construção das tábuas-modelo a partir dela. Na Figura 3, há uma amostra de 6 das 47 probabilidades de morte para cada sexo: duas extremas (Níveis 1 e 47) e quatro intermediárias (Níveis 7, 17, 27 e 37).
Relação entre as esperanças de vida masculinas e femininas
Para cada uma das 40 macrorregiões que deram origem às tábuas-modelo de mortalidade, como se explicou nos pontos anteriores, foram geradas esperanças de vida ao nascer ajustadas para cada sexo. Esses dois conjuntos de 40 esperanças de vida ao nascer foram colocados lado a lado, em formato de gráfico. Observou-se a existência de uma relação praticamente linear entre ambos, com tendência a aumentar as suas diferenças conforme cresce o seu valor, fato condizente com o que se conhece a respeito das tendências em outros países. A correlação encontrada entre eles foi de 0,975, o que autorizou a adoção da seguinte função linear, que relaciona as esperanças de vida masculinas e femininas:

A seguir, especificam-se os procedimentos adotados para gerar as tábuas-modelo para homens, para mulheres e para ambos os sexos:
- criação das tábuas-modelo por meio da função logística obtida para o sexo masculino, a partir de uma esperança de vida ao nascer de 50 anos, até 73 anos – de meio em meio ano –, em um total de 47 níveis diferentes;
- geração das 47 esperanças de vida ao nascer femininas correspondentes às masculinas, por meio da função descrita anteriormente;
- criação das tábuas-modelo por meio da função logística encontrada para o sexo feminino, a partir das esperanças de vida ao nascer previamente definidas; e
- criação das tábuas-modelo para ambos os sexos (utilizando-se a relação de 105 nascimentos masculinos para 100 femininos), a partir das tábuas-modelo masculinas e femininas.
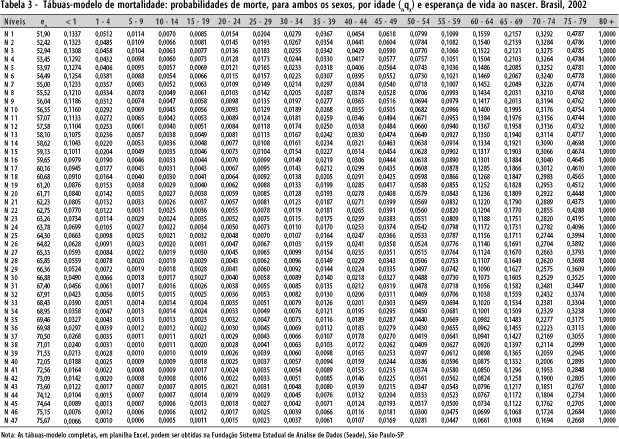
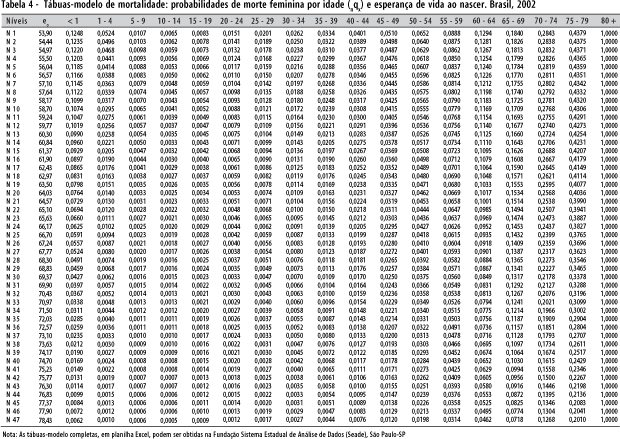
As probabilidades de morte das tábuas-modelo de mortalidade encontram-se nas tabelas 3, 4 e 5.
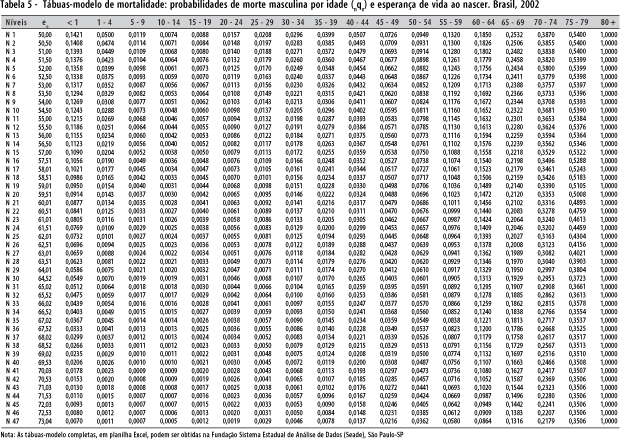
O modelo das causas externas e aids
Como já foi justificado, a proposta de tábuas-modelo de mortalidade exclui as mortes por causas externas e aids. Assim, foi necessário criar um modelo adicional, a ser sobreposto ao das tábuas-modelo de mortalidade, para completar as probabilidades de morte por idades.
Ao observar a influência das causas externas e da aids por sexo e idades na mortalidade, chegou-se às seguintes conclusões (Figura 4 e Tabela 6):
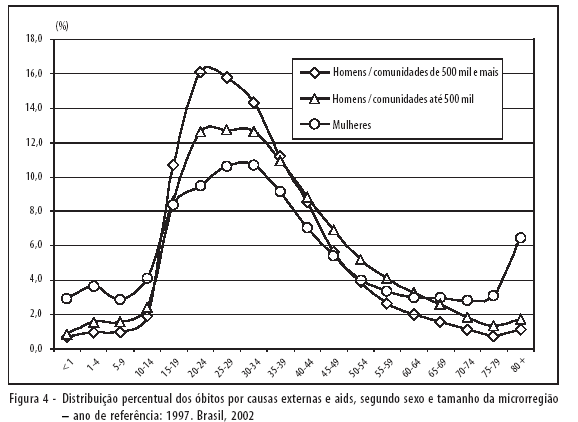
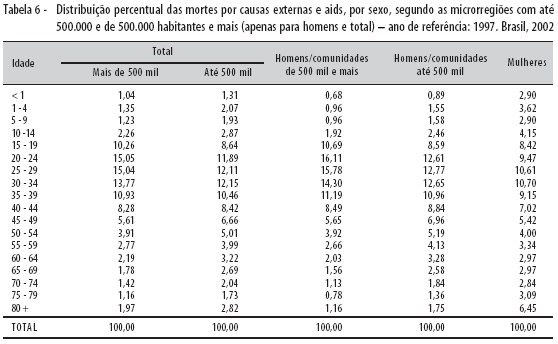
a) A proporção de mortes por idades, tanto para homens como para mulheres, tem um sentido ascendente até as idades adultas jovens; e descendente a partir daí, com pequeno aumento nos últimos anos de idade.
b) Nos homens, foram encontrados dois comportamentos diferentes: um, típico de microrregiões até 500.000 habitantes; e outro, de microrregiões com 500.000 habitantes e mais.
c) Ainda no caso do sexo masculino, os níveis das probabilidades de morte são sensivelmente menos elevados no contexto das pequenas aglomerações.
d) Finalmente, ainda com referência aos homens, a porcentagem das mortes também difere segundo o tamanho da localidade: nas comunidades de 500 mil habitantes e mais, essas porcentagens são sensivelmente mais elevadas nos grupos de adultos jovens.
Frias,21 mediante avaliação empírica, constatou que "...o sub-registro dos óbitos violentos é inferior ao das causas naturais". Isso se deve ao fato de que a vítima passa, quase sempre, por perícia médica.
A partir das observações anteriores, é de se supor que essas proporções sejam utilizadas para o cálculo de taxas de óbitos por causas externas e aids, por sexo e idades, questão a ser abordada no item seguinte.
Resultados
Aplicação das tábuas-modelo
O princípio fundamental do modelo proposto é que, no Brasil, ao contrário do que se esperava inicialmente, há um só padrão básico de mortalidade; ou seja, as mudanças nas porcentagens das taxas de mortalidade (ou probabilidades de morte), caso aumente o nível de esperança de vida ao nascer, são paulatinas e previsíveis, de tal forma que a construção de tábuas-modelo de mortalidade para o país torna-se factível. Dito de outra forma, basta uma só estimativa de taxa de mortalidade por idade (ou probabilidade de morte por idade) como condição para estimar as taxas nas outras idades e, por conseqüência, a esperança de vida ao nascer. Todavia, como já foi observado, as taxas de mortalidade por causas externas e aids perturbam esse cálculo porque seguem um padrão dependente do sexo, das idades e do tamanho das cidades.
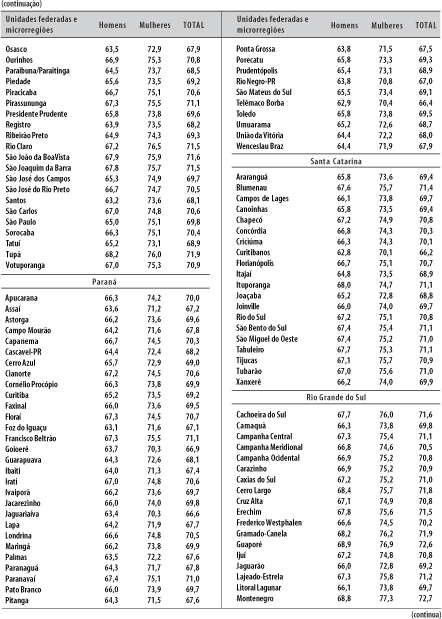
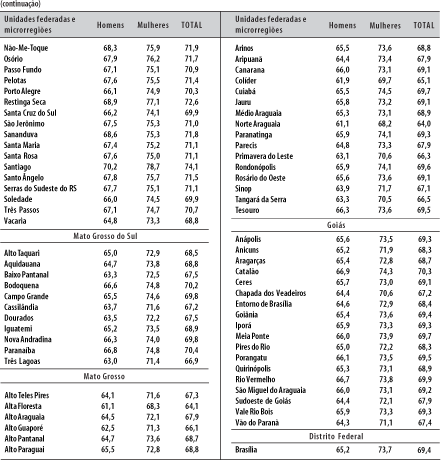
Por outro lado, a única estimativa confiável de mortalidade para todas as microrregiões (e alguns Municípios) no país, atualmente, é a de mortalidade infantil (probabilidade de morte dos menores de um ano), fato já citado. Está claro que essas estimativas são mais confiáveis na medida em que aumenta o tamanho da unidade territorial, como é o caso dos Estados, etc. Por essa razão, a título de exemplo de aplicação e para avaliar a robustez e coerência do modelo proposto, foi estimada a esperança de vida ao nascer das unidades federadas a partir de suas taxas de mortalidade infantil. Todos os anos, o próprio Ministério da Saúde, por intermédio da Ripsa, estima a esperança de vida ao nascer dessas mesmas unidades, acessível em fonte já citada.7
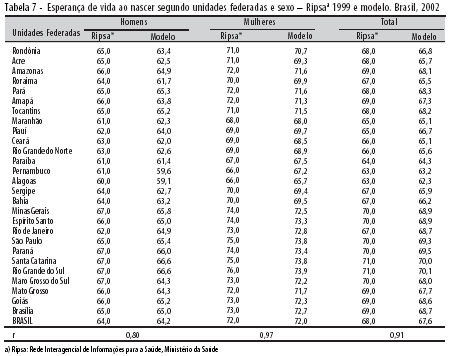
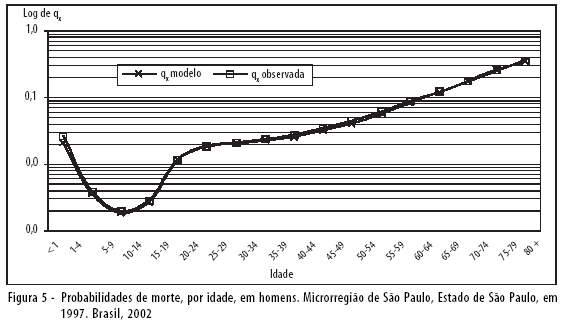
Ao aplicar as taxas de mortalidade infantil dos Estados no modelo, pode-se estimar as taxas e/ou probabilidades nas outras idades. Porém, há que ressalvar, novamente, que o modelo exclui as causas externas e a aids; e que, no caso da mortalidade infantil, essas causas têm importância ínfima (em torno de 1%). Encontrado o nível dessa mortalidade infantil no modelo, basta calcular as taxas por causas externas e aids dos Estados e somá-las às do modelo. Na Tabela 7, encontram-se as esperanças de vida assim calculadas, comparadas com as adotadas pela Ripsa. Os resultados são muito similares, principalmente para o sexo feminino. Deve-se levar em consideração que a Ripsa calcula a esperança de vida de maneira similar, mas com tábuas-modelo já superadas. Para exemplificar os resultados por grupos etários, mostram-se, na Figura 5, as probabilidades de morte por idades da população masculina da Microrregião de São Paulo, segundo o SIM (cujas estatísticas de óbitos são, reconhecidamente, de boa qualidade) e o modelo: os resultados são muito similares, o que reforça ainda mais a solidez do modelo proposto.
Para microrregiões ou Municípios com menos de um milhão de habitantes, o cálculo das probabilidades de morte por causas externas e aids deve ser feito com a utilização do modelo de causas externas e aids, de tal forma a evitar as oscilações devidas aos pequenos números (nas localidades maiores, como já se viu, podem-se calcular as taxas diretamente com os dados do registro civil). Os passos para o cálculo da mortalidade nessas unidades menores são:
a) Encontrar a mortalidade infantil da microrregião ou Município, fornecida para ambos os sexos (Ministério da Saúde, fonte já citada).
b) Procurar, no modelo para ambos os sexos, o nível correspondente à mortalidade infantil encontrada (com o que se chega às probabilidades de morte por idades e, por conseqüência, às taxas de mortalidade por idades). Se se desejam as probabilidades para homens e mulheres separadamente, basta procurá-las nos mesmos níveis, agora nas tabelas para homens e/ou mulheres.
c) Procurar o número total de mortes por causas externas e aids para a população total (de ambos os sexos; ou para os sexos separados), fornecida pelo registro civil.
d) Distribuir esse número segundo as proporções do modelo de causas externas e aids, para a população total ou por sexo e o tamanho da localidade.
e) Calcular as taxas de mortalidade por causas externas e aids por idades.
f) Somar essas taxas às de mortalidade do nível adequado do modelo, obtido no passo b), para obter as taxas de mortalidade por todas as causas.
g) Calcular, a partir dessas taxas, as outras funções da tábua de mortalidade (probabilidades de morte por idades, esperança de vida ao nascer, etc.), segundo a conveniência.
É importante ressaltar que, na medida em que se obtenham novos dados sobre mortalidade em outras idades que não a infantil, principalmente por estimativas indiretas a partir do Censo Demográfico de 2000, poder-se-á calcular, de maneira mais confiável ainda, os níveis de mortalidade dos Estados, microrregiões, etc.
Cálculo da mortalidade por microrregiões
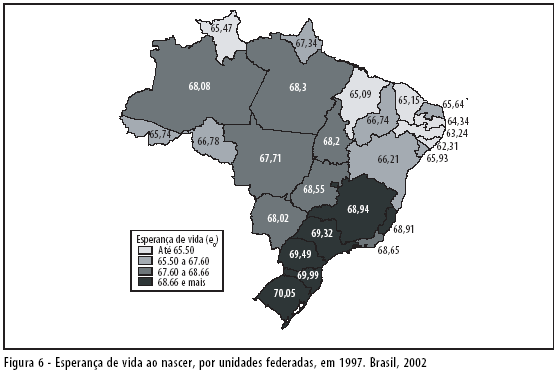
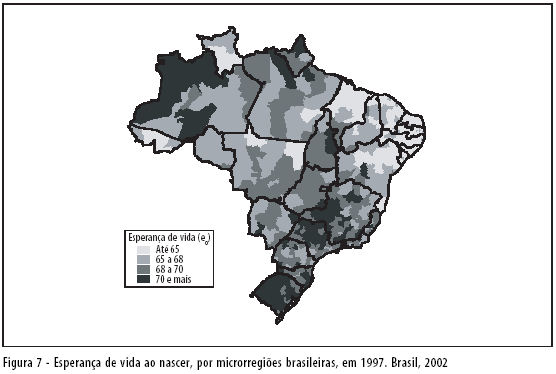
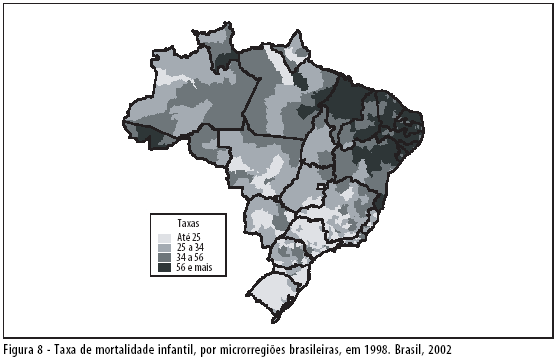
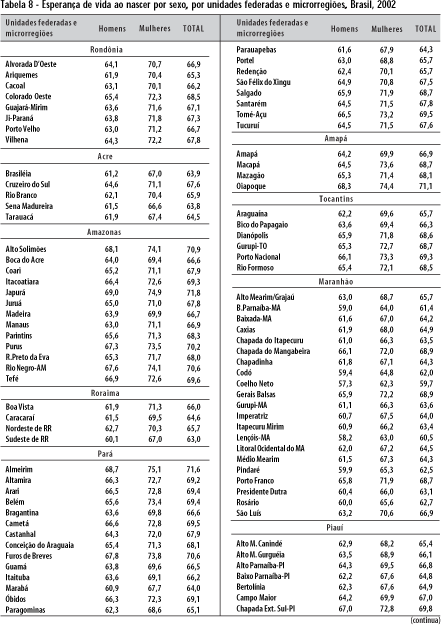
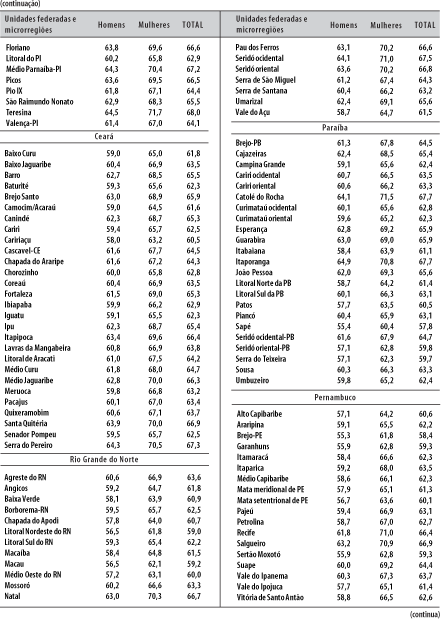
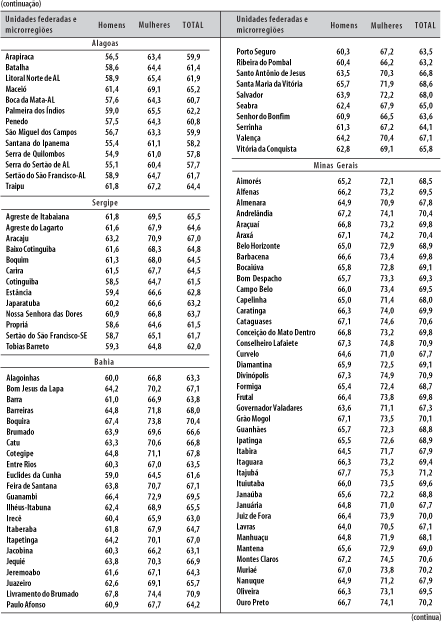
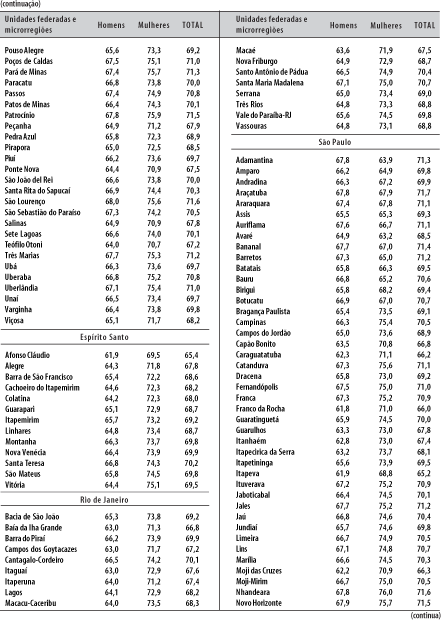
Seguindo os passos descritos no ponto anterior, são calculadas as taxas de mortalidade por idades ou as probabilidades de morrer por idades e as respectivas esperanças de vida por microrregiões. Os resultados podem ser visualizados nas figuras 6, 7 e 8 e na Tabela 8. As figuras de números 7 e 8 são muito parecidas: nesse caso, as esperanças de vida foram obtidas a partir das taxas de mortalidade infantil já existentes e divulgadas pelo Ministério da Saúde, em fonte já citada.7
Discussão
As taxas aqui utilizadas foram calculadas a partir de dados populacionais por sexo e idades projetados pelo IBGE a partir de censos demográficos e da Contagem de 1996. Com a publicação dos resultados do Censo Demográfico de 2000, poder-se-ão recalcular essas taxas, atualizando-as, o que, eventualmente, ocasionará pequenas modificações no modelo proposto.
Todo e qualquer modelo deve, sempre, ser encarado com ressalvas, porque está sujeito a caducidade. As estruturas de mortalidade por sexo e idades mudam com o avanço do tempo e/ou da tecnologia, do surgimento da epidemia de aids, como também do aumento da violência urbana e do rápido declínio da mortalidade infantil no Brasil, nos últimos anos.
No modelo apresentado por este estudo, há duas particularidades que devem ser especialmente observadas de maneira crítica, apesar de terem sido adotadas para a solução de problemas reais encontrados no decorrer da pesquisa. Em primeiro lugar, a de que as causas violentas e a aids foram eliminadas do modelo original (Tabela 3), procedimento que, segundo investigação dos autores, nunca antes foi feito. Em segundo lugar, a utilização da função logística para suavizar as curvas de mortalidade das 40 macrorregiões também é inédita nesses modelos. Devem-se, portanto, confrontar os resultados do modelo com novos dados e tentativas de cálculo da mortalidade a partir de diferentes metodologias, principalmente nas regiões onde são necessários cálculos indiretos da mortalidade, ou seja, o Norte e o Nordeste do país.
Finalmente, a partir dos dados indiretos sobre mortalidade do Censo Demográfico de 2000 – e, inclusive, de outras fontes futuras, como a Pesquisa Nacional por Amostras de Domicílio-PNAD/IBGE, etc. –, poder-se-ão elaborar novas e mais consistentes estimativas de esperanças de vida e de mortalidade por sexo e idades, utilizando-se o modelo proposto. As estimativas aqui apresentadas tiveram por base o único indicador de mortalidade disponível no momento: a mortalidade infantil.
Agradecimentos
Participaram diretamente do projeto "Desenvolvimento de Metodologias Alternativas para a Análise de Bancos de Dados Secundários", no qual estão inseridos os resultados deste artigo, os seguintes pesquisadores, listados em ordem alfabética:
- Ana Celeste Cruz - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Clóvis de Araújo Peres - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Eliana Monteiro Rodrigues - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Francisco Torres Troccoli - Secretaria de Estado da Saúde de São Paulo, São Paulo-SP
- Gustavo Coelho de Souza - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Haroldo da Gama Torres - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo- SP
- Irineu F. Barreto Junior - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Maria Paula Ferreira - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Nádia Pinheiro Dini - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Maria Helena P. de Mello Jorge - Universidade de São Paulo-USP, São Paulo-SP
- Maria Lúcia Lebrão - Universidade de São Paulo- USP, São Paulo-SP
- Zilda Pereira da Silva - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
Participaram da parte do estudo referente à mortalidade, que originou o presente artigo, os seguintes pesquisadores, listados em ordem alfabética:
- Cecília Polidoro Mameri - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Luiz Armando de Medeiros Frias - Fundação Instituto Brasileiro de Geografia e Estatística (IBGE) (in memoriam)
- Maria Graciela Gonzales Morell - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
- Rute Eduviges Godinho - Fundação Sistema Estadual de Análise de Dados-Seade, São Paulo-SP
Referências bibliográficas
1. Fundação Seade. Desenvolvimento de metodologias alternativas para a análise de bancos de dados secundários. Relatório final. São Paulo: Fundação Seade; 2001.
2. Fundação Instituto Brasileiro de Geografia e Estatística. Brasil: tábuas-modelo de mortalidade e populações estáveis. Rio de Janeiro: IBGE; 1981.
3. Coale AJ, Demeny P. Regional model life tables and stable populations. New York: Academic Press; 1985.
4. United Nations. Model life tables for under-developed countries. New York: United Nations; 1955.
5. United Nations. Model life tables for developing countries. New York: DIESA, ST/ESA/SER.A/77; 1982.
6. Lerdermann S. Nouvelles tables-type de mortalité. Travaux et documents, Institut National d’Études Démographiques 1969;53.
7. Ministério da Saúde. Rede Interagencial de Informações para a Saúde. Indicadores de Dados Básicos para a saúde no Brasil (IDB 2001). Brasília: MS; 2001 [Monografia na Internet] Disponível em http://tabnet.datasus.gov.br/cgi/idb2002/public.htm
8. Vasconcelos AMN. Qualidade das estatísticas de óbitos no Brasil: uma classificação das Unidades da Federação. In: Anais do XII Encontro Nacional de Estudos Populacionais; 2002; Ouro Preto, MG. Belo Horizonte: ABEP; 2002. Vol 1.
9. Brito ALS, Rodrigues EM. Diagnóstico das internações hospitalares. In: Fundação Seade: 20 Anos no Ano 2.000 - Estudos sociodemográficos sobre a juventude paulista. São Paulo: Fundação Seade; 1998. p.84-100.
10. Buss PM. Assistência hospitalar no Brasil, 1984-1991. Uma análise preliminar baseada no sistema de informação hospitalar do SUS. Informe Epidemiológico do SUS 1993;2:5-17.
11. Carvalho DM. Grandes sistemas nacionais do SUS – v. 4. Rio de Janeiro; 1997.
12. Ferreira JMN. Mortalidade hospitalar no Estado de São Paulo. São Paulo em Perspectiva 1986;2(2/3):31-52.,
13. Lebrão ML. Análise da fidedignidade dos dados estatísticos hospitalares disponíveis na Secretaria de Estado da Saúde de São Paulo em 1974. Revista de Saúde Pública 1978;12:234-248.
14. Mello Jorge MHP, Gotlieb SLD, Oliveira H. O Sistema de Informação sobre Nascidos Vivos – Sinasc. São Paulo: Centro da OMS para a Classificação de Doenças em Português - Núcleo de Estudos em População e Saúde - USP; 1992. Série Divulgação n. 7.
15. Adams SJ. Projecting the next decade in Safety Management - A Delphi Technique Study [Abstract on the Internet] Avaiable from http://www.asse.org/ps1001_adams.pdf
16. Simões C. Estimativas da mortalidade infantil por microrregiões e municípios. Brasília: Ministério da Saúde; 1999.
17. Programa de las Naciones Unidas para el Desarrollo. Informe sobre el Desarrollo Humano 2003 – Notas técnicas [Monografía en la Internet] Disponible en http://www.undp.org
18. Figoli MGB, Wong LLR. O processo de finalização da transição demográfica na América Latina. In: Anais do XII Encontro Nacional de Estudos Populacionais; 2002; Ouro Preto, MG. Belo Horizonte: ABEP; 2002. Vol 1.
19. Mello Jorge MH, Gotlieb SLD. As condições de saúde no Brasil: retrospecto de 1979 a 1995. Rio de Janeiro: Editora Fiocruz; 2000.
20. Barreto ML, Carmo EH. Mudanças em padrões de morbimortalidade: conceitos e métodos. In: Monteiro CA, editor. Velhos e novos males da saúde no Brasil: a evolução do país e de suas doenças. São Paulo: Hucitec; 1995. p.17-30.
21. Frias LAM. Uma proposta de metodologia para avaliação da cobertura dos óbitos registrados por causas violentas. In: Anais do XII Encontro Nacional de Estudos Populacionais; 2000; Caxambu, MG. Belo Horizonte: ABEP; 2000. Vol. 2.
 Endereço para correspondência:
Endereço para correspondência:
Fundação Seade
Av. Cásper Líbero, 464
São Paulo-SP.
CEP: 01033-000
E-mail:paulocampanario@uol.com.br e pmaia@seade.gov.br
*Pesquisa demandada por meio de edital e apoiada com recursos do Projeto Vigisus, Secretaria de Vigilância em Saúde, Ministério da Saúde.