Introdução
A COVID-19, doença decorrente da infecção pelo vírus Sars-CoV-2, entre outras manifestações clínicas, pode incluir a síndrome respiratória aguda grave (SARS). 1 O primeiro caso no Brasil foi confirmado no dia 25/2/2020; em 3/5/2020, o país já contava, oficialmente, mais de 100 mil casos e 7 mil óbitos. 2 Dado seu amplo alcance e rápida propagação, seu potencial de levar a rede hospitalar ao colapso, sobretudo à disponibilidade insuficiente de leitos em unidades de terapia intensiva (UTI), a COVID-19 é considerada uma condição muito grave para a Saúde Pública. 1
Embora existam relatos de experiências com tratamentos e iniciativas para a obtenção de uma vacina, até o momento desta publicação, não havia comprovação robusta de eficácia de intervenções farmacológicas na prevenção ou tratamento dessa condição clínica. 3 A ampla testagem, a proteção de profissionais (serviços de saúde e serviços essenciais), o isolamento de indivíduos infectados e a adoção de intervenções não farmacológicas, como as políticas públicas de distanciamento social, apresentam-se como a opção mais factível de abordagem da COVID-19. 4 No dia 11/3/2020, com vigência em todo o Distrito Federal do Brasil, foram decretadas as primeiras medidas locais de distanciamento social diante do risco da infecção pelo novo coronavírus, incluindo a suspensão de eventos com público superior a 100 pessoas e as atividades educacionais em todas as escolas, universidades e faculdades. 5 Adicionalmente, bares e restaurantes deveriam garantir a distância mínima de dois metros entre as mesas. Na data de 21/4/2020, além das medidas já aplicadas, o governo do Distrito Federal passou a adotar a testagem populacional de indivíduos sintomáticos, ampliando postos de coleta e triagem fora das unidades de saúde, exclusivamente para essas pessoas.
Com o intuito de monitorar e orientar as decisões de políticas públicas voltadas à COVID-19, uma série de iniciativas e redes têm unido esforços e disponibilizado ferramentas de predição de casos, projeção de necessidade de leitos e de equipamentos hospitalares. 6-8 Nesse aspecto, a análise de dados sobre políticas públicas, no que diz respeito à avaliação de seu impacto, é um campo de possíveis inferências, para as quais são indispensáveis dados robustos. Em cenários com limitação temporal na disponibilidade de dados, é de grande valor a construção de modelos e contrafactuais (cenários possíveis, não necessariamente observados) para identificar tendências e projeções dos possíveis impactos de uma determinada política pública. 9
Tomando por base o contexto da ocorrência de casos de COVID-19 na população do Distrito Federal, o objetivo deste estudo foi construir cenários para analisar o impacto das políticas de distanciamento social na propagação da COVID-19 e a necessidade de leitos em UTIs, com o auxílio de um modelo matemático e simulações de Monte Carlo.
Métodos
Tendo como referência os fundamentos e delineamentos de pesquisas no campo da avaliação de políticas públicas, 9 trata-se de um estudo de caso, pautado em simulações. Após a coleta de dados e indicadores, foram construídos cenários de projeções e contrafactuais, relevantes para a análise do impacto das medidas de distanciamento social sobre a demanda por leitos de UTI no contexto observado.
Como caso desta análise, considera-se a conformação de todas as regiões administrativas integrantes do Distrito Federal, cuja população total é estimada em 3.223.048 habitantes para 2020, de acordo com projeções do Instituto Brasileiro de Geografia e Estatística (IBGE). 10 No intuito de obter uma referência da capacidade hospitalar instalada, foi consultado o número de leitos de UTI-adulto cadastrados na região, segundo o banco de dados do Cadastro Nacional de Estabelecimentos de Saúde (CNES) disponível até o mês de junho de 2020. Complementarmente, visando contextualizar a adesão da população às medidas de distanciamento social recomendadas pelas políticas instituídas, foram consultados os dados públicos do ‘índice de isolamento social’ no Distrito Federal, referentes ao período de 1/3/2020 a 31/7/2020, disponibilizados pela empresa de tecnologia Inloco. 11 Tal indicador tem auxiliado iniciativas de monitoramento da propagação da COVID-19, desenvolvidas por universidades públicas e instituições governamentais. Fazendo uso de dados de geolocalização de dispositivos telefônicos de uma parcela da população local - mediante autorização prévia -, é possível estimar, diariamente, o percentual dessa população que tem acatado as orientações públicas de isolamento social. 11
Estrutura do modelo
Para estimar a necessidade de leitos de UTI decorrente da propagação da doença, construiu-se um modelo matemático. Adotada a diretriz metodológica publicada pela Secretaria de Ciência, Tecnologia e Insumos Estratégicos do Ministério da Saúde 12 e os fundamentos práticos da modelagem de doenças infecciosas, 13 decidiu-se pela concepção de um modelo compartimental de transição dinâmica. Neste modelo, derivado da clássica proposta do modelo SIR (sigla para ‘suscetíveis, infectados e recuperados’) proposto por Kermack e McKendrick, a transição entre os compartimentos (ou estados de saúde) é representada por um sistema de equações diferenciais dependentes, entre outros parâmetros, de número de infectados ( I ), coeficiente de transmissão ( β ), latência ( α ) e recuperação ( γ ).
Adotou-se, neste trabalho, uma estrutura de transições e compartimentos orientada por modelos disponibilizados previamente, por outros autores que também buscavam a projeção da demanda hospitalar, 14-16 além do impacto de intervenções não farmacológicas - como o uso de máscaras - sobre a propagação comunitária da COVID-19. 17 Nesta proposta, o modelo para a relação diária entre o número de indivíduos suscetíveis ( S ), expostos ( E ), infectados ( I ) e removidos ( R ) - SEIR - é representado na Figura 1 .
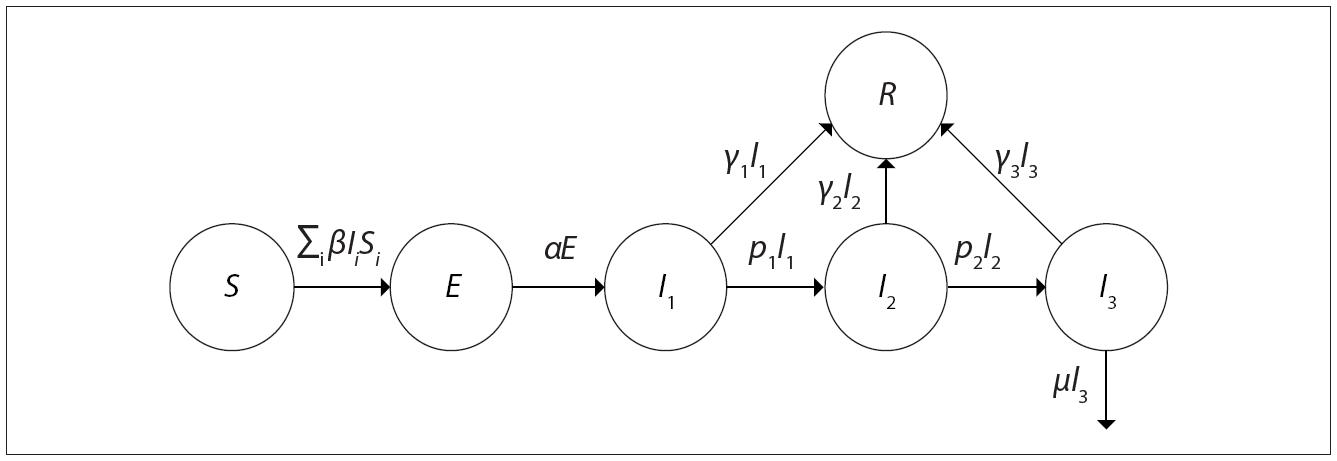
Fonte: Adaptado de Hill. 15
Figura 1 Representação da estrutura do modelo dinâmico compartimental adotado
Dentro do compartimento de infectados, são ainda consideradas as subdivisões dos indivíduos que não necessitam de hospitalização ( I1 ), aqueles que evoluem para a necessidade de hospitalização ( I2 ) e, por fim, os pacientes com quadro crítico ( I3 ) que evoluem para a necessidade de internação em UTI.
Principais premissas do modelo
Não é prevista a mudança do tamanho total da população (natalidade e mortalidade geral), exceto pela morte por COVID-19. Dado o curto horizonte temporal de análise, considerou-se que tal restrição simplificaria o modelo, com pouco impacto nos resultados.
Semelhantemente a abordagens prévias, baseadas em modelos SEIR da COVID-19, 17 assume-se que os indivíduos hospitalizados não estejam efetivamente expostos à população geral e, portanto, não contribuam para o cálculo da força de infecção na comunidade.
Não é prevista a possibilidade de reinfecção de um indivíduo recuperado, ainda que não existam evidências definitivas sobre o grau com que a imunidade adquirida, após a infecção de fato, proteja-o de reinfecção. 18
Não sendo objetivo da análise, o presente modelo desconsidera o potencial aumento da mortalidade devido à falta de leitos. É mister considerar que a letalidade observada no modelo possa estar subestimada em um cenário de indisponibilidade de leitos.
As estimativas de contato efetivo assumem o pressuposto da mistura homogênea ( random mixing ), 13 onde cada indivíduo infectado possa entrar em contato com um indivíduo suscetível de acordo com a mesma probabilidade média.
As equações completas e mais detalhes sobre o modelo estão disponíveis no Material Suplementar 1.
Cenários
No horizonte temporal de 1 ano, período considerado suficiente para abarcar tanto uma onda completa de infecções como a incerteza sobre a disponibilidade ou não de futuras intervenções específicas (vacinas e tratamentos), tomando-se como referencial a data inicial de 22/3/2020, dada a margem de dez dias entre o início das medidas de distanciamento social e o pico dos níveis de isolamento social obtido no Distrito Federal, foram construídos três cenários de propagação da COVID-19, visando analisar o impacto potencial da doença sobre a necessidade de atendimento hospitalar.
Cenário A - Perfil de propagação sem adesão às medidas de distanciamento social
Definição
Representa o contrafactual do que ocorreria se não fossem tomadas ou aderidas pela população as medidas de distanciamento social.
Para tanto, ao longo do modelo, não é inferida nenhuma redução do contato social, adotando-se a estimativa média de isolamento social observada nos últimos dez dias antes do decreto local de 11/3/2020.
Assim, adota-se um valor constante para o coeficiente de transmissão ( β ) no modelo.
Cenário C - Perfil de propagação com a dinâmica observada de queda do nível de distanciamento social
Definição
Representa a dinâmica de isolamento social observada no Distrito Federal e a possível projeção da necessidade de leitos com a manutenção dos últimos níveis médios de isolamento observados.
Neste contexto, buscando simular uma interrupção ou retorno das medidas de distanciamento, são também estimadas metas de isolamento populacional de acordo com a demanda por leitos de UTI.
Conforme observado nas definições apresentadas, não foi prevista a simulação completa de cenários com uma adesão ao distanciamento acima da média observada após a implementação das políticas de distanciamento. Apesar disso, ressalta-se que a análise de metas de isolamento prevista no Cenário C não teve tal restrição.
Valores dos parâmetros e incertezas
Com o intuito de aproximar o modelo de análise à realidade local e ao tamanho da população, tomou-se a estrutura etária do Distrito Federal para o ajuste dos indicadores esperados de letalidade e hospitalização para a região. A partir dos boletins oficiais da Secretaria de Estado de Saúde do Distrito Federal, 19 foram levantados os números de casos por data de início de sintomas, internações em UTI e óbitos por COVID-19. Além das estimativas de infecção e letalidade por faixa etária para o Distrito Federal (Material Suplementar 2), a série completa de internações em UTI, óbitos e percentual de isolamento social disponíveis para o período de análise (dados de 1/3/2020 a 31/7/2020) é apresentada no Material Suplementar 3. Além dos parâmetros citados, para cada cenário estimou-se a evolução diária do número de reprodução instantâneo (Rt)
Na ausência de dados locais dos demais parâmetros, utilizando-se de uma adaptação da estrutura básica de busca com os termos (COVID-19 OR coronavirus) AND ( model OR modelling ), foram também consultadas publicações indexadas na base Pubmed ( http://www.ncbi.nlm.nih.gov/pubmed ), prévias de publicações na base MedRvix ( www.medrxiv.org ) e repositórios públicos de parâmetros de modelagem, como a iniciativa da rede MIDAS ( http://midasnetwork.us/COVID-19 ). A escolha das fontes de dados dos parâmetros disponíveis priorizou aquelas utilizadas em modelos validados por outras instituições de referência no tema, como os modelos do Imperial College London, buscando a comparabilidade do modelo aqui proposto. Os dados extraídos incluíram as estimativas pontuais e suas incertezas paramétricas (erros-padrão, intervalos de confiança ou distribuições de probabilidade). Os valores dos principais parâmetros considerados no modelo aqui proposto, acompanhados de sua incerteza paramétrica, descrição e fontes, são apresentados na Tabela 1 .
Tabela 1 Relação de valores, incertezas paramétricas, distribuições e fontes dos principais parâmetros do modelo de propagação da COVID-19 no Distrito Federal, Brasil
| Parâmetro | Estimativa pontual | Limite inferior | Limite superior | Função de probabilidade | Descrição | Fonte |
|---|---|---|---|---|---|---|
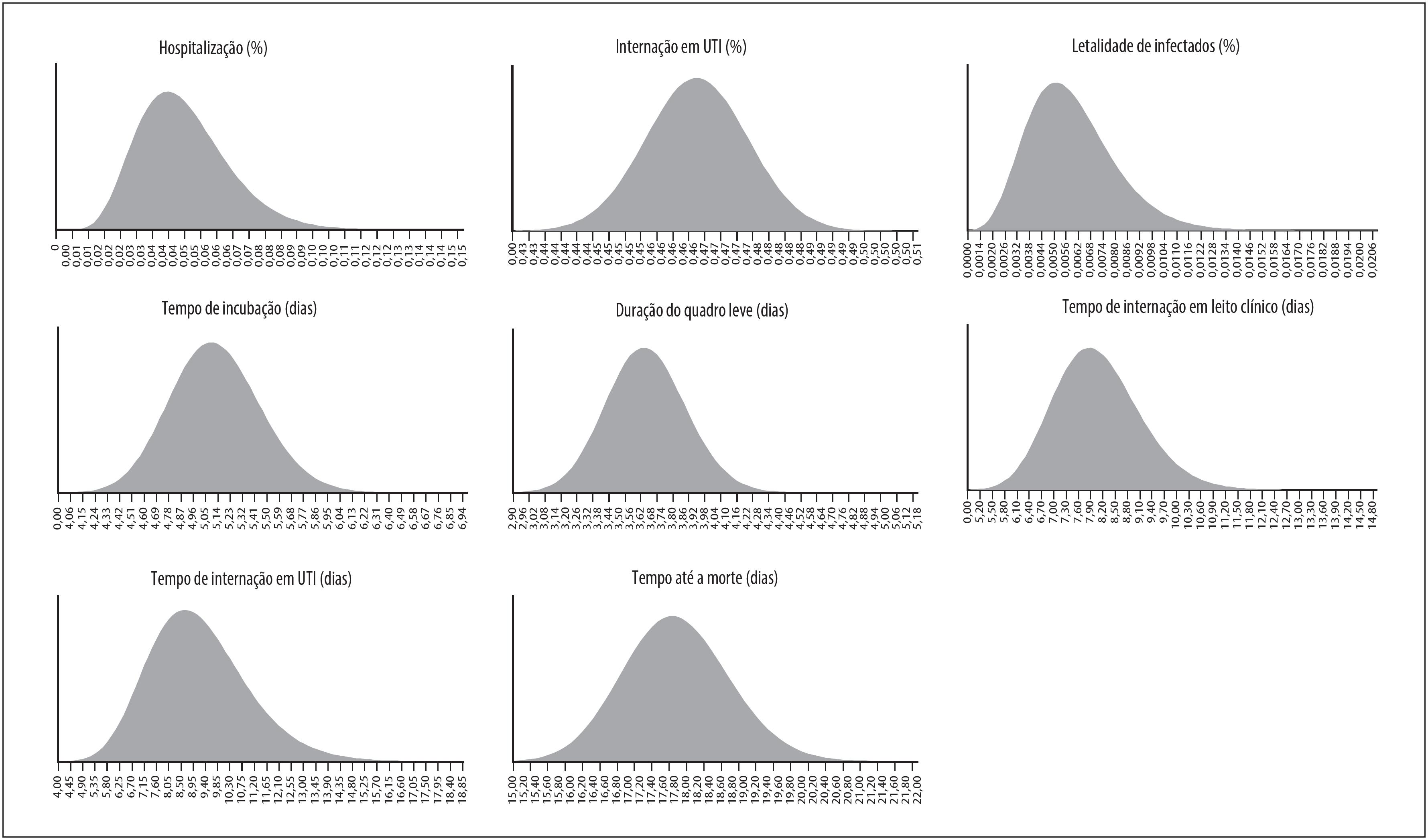
| Incubação (dias) | 5,10 | 4,50 | 5,80 | Lognormal | Tempo de incubação | Sanches et al. 26 |
| Duração - leve (dias) | 3,65 | 3,21 | 4,09 | Gama | Duração do quadro até isolamento ou hospitalização | Linton et al. 27 |
| Quadro grave (%) | 4,57 | 2,72 | 9,32 | Beta | Proporção de infectados que terão quadro grave ou crítico (hospitalização) | Verity et al. 28 |
| Tempo de internação (dias) | 8,00 | 6,00 | 10,00 | Lognormal | Tempo médio de internação em enfermaria | Ferguson et al. 29 |
| Internação em UTI a (%) | 46,30 | 44,31 | 48,06 | Beta | Percentual de pacientes graves que necessitam de cuidados intensivos | Boletins Epidemiológicos 19 |
| Tempo em UTI (dias) | 9,00 | 6,00 | 13,00 | Lognormal | Tempo médio de internação em UTI a | Grasselli et al.(30) |
| Letalidade (%) | 0,576 | 0,315 | 1,140 | Beta | Letalidade de infectados ajustada para a região | Verity et al. 28 |
| Tempo até a morte (dias) | 17,80 | 16,02 | 19,58 | Lognormal | Tempo médio do início dos sintomas até a morte | Verity et al. 28 |
| Mortalidade na UTI a (%) | 27,23 | 12,85 | 47,81 | Não se aplica | Probabilidade de morte em UTI a | Calibrado pela letalidade |
a)UTI: unidade de terapia intensiva.
Para considerar o impacto das incertezas paramétricas dos nove parâmetros descritos na Tabela 1 , sobre os resultados do modelo, as análises foram conduzidas em uma abordagem estocástica (probabilística), fazendo-se uso de simulações de Monte Carlo, sendo conduzidos múltiplos sorteios em nível de valor esperado (2ᵃ ordem). 20 Com base nas características das variáveis, foram ajustadas distribuições a priori de probabilidade para os parâmetros de tempo de incubação (dias), duração do quadro leve (dias), fração de indivíduos com quadro grave (%), tempo de internação em enfermaria (dias), fração de indivíduos que evoluem para internação em UTI (%), tempo de internação em UTI (dias), letalidade (%) e tempo do início dos sintomas até a morte (dias), conforme ilustrado no Material Suplementar 4. Na ausência de intervalos nas fontes de dados, considerou-se a reamostragem com reposição ( bootstrap ) para estimar a incerteza paramétrica (intervalos de confiança). Os resultados foram resumidos em medianas e amplitudes de cobertura das simulações (intervalo interqualil [IIQ] e intervalo de confiança [IC]).
Validação
Para a calibração do modelo, adotou-se a referência do cenário que reflete a propagação durante os níveis de distanciamento social observado (Cenário C). Foram registrados os valores da estatística da minimização da raiz quadrada do erro médio (RMSE) do número de óbitos preditos pelo modelo, observados na série temporal em análise. A adequação do número de simulações de MC foi avaliada com a inspeção visual da convergência dos principais parâmetros do modelo.
Todas as análises foram conduzidas com auxílio do software Microsoft Excel® e da linguagem de programação Visual Basic for Applications (VBA). O ajuste dos parâmetros de calibração foi realizado com o método dos mínimos quadrados não linear, com apoio do algoritmo de otimização Generalized Reduced Gradient (GRG) não linear, implementado na função SOLVER. O modelo completo e seu histórico de versões estão disponíveis em um repositório público de dados. 21
Resultados
Conforme as fontes oficiais consultadas, do período de 1/3/2020 até a data final de obtenção de dados para o modelo, 31/7/2020, havia-se confirmado 106.292 casos e 1.469 óbitos por COVID-19 no Distrito Federal. 19 Ao se considerar a data do primeiro decreto local sobre as medidas de distanciamento, foi possível observar uma importante adesão inicial da população às medidas, dado o aumento gradual do índice de isolamento social ao longo dos dias seguintes ao decreto, de uma média de 30,0% entre 2/3/2020 e 11/3/2020, para uma média de 57,4% entre 22/3/2020 e 30/4/2020 ( Figura 2 ).
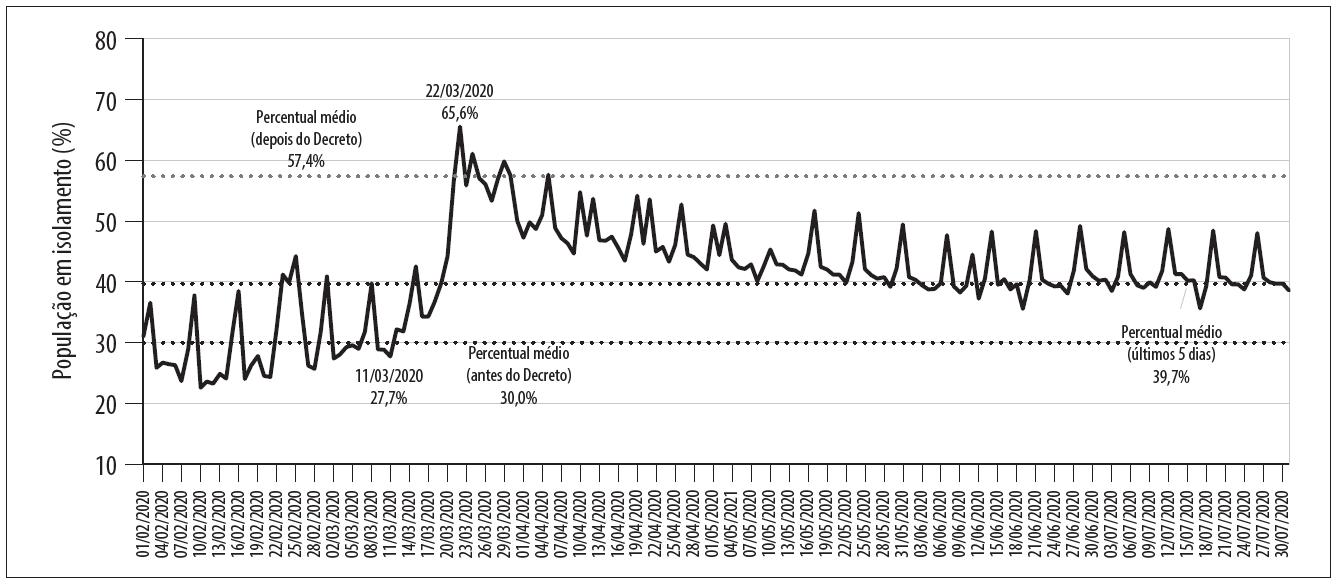
Fonte: dados da base pública da InLoco. 11
Figura 2 Evolução do percentual de isolamento social de acordo com a data da implementação das medidas de enfrentamento à COVID-19 no Distrito Federal, Brasil
Considerando-se os registros de casos segundo a data de início dos sintomas, todos os cenários iniciaram as simulações na data de 22/3/2020, com uma estimativa média de 366 indivíduos infectados (I1) e 732 expostos (E) - dada a existência de um número de reprodução instantâneo (Rt) mínimo de 2 sem o isolamento social. Com um RMSE de 83,5 nos valores preditos de óbitos, o valor do parâmetro τ foi estimado em 0,6979 na calibração do modelo. De acordo com o banco de dados do CNES, o Distrito Federal possuía, até o mês de junho, um total de 1.534 leitos de UTI-adulto, 378 deles públicos. A seguir, são apresentados os resultados de cada um dos cenários.
Cenário A - Perfil de propagação sem adesão às medidas de distanciamento social
No primeiro cenário, o coeficiente de transmissão é calculado assumindo-se um nível de isolamento social de 30,0%, coerente com os valores médios observados até a data de 11/3/2020. Como ilustrado na Figura 3 , dada a necessidade de hospitalização dos casos críticos, sem a adesão da população ao distanciamento social, haveria um pico de necessidade, com a mediana das simulações, em 6.214 internações em UTI (IIQ: 4.618 a 8.415) na data provável de 14/7/2020 (IIQ: 9/7/2020 a 20/7/2020). No entanto, de acordo com os dados do CNES, o número total de leitos públicos de UTI cadastrados já teria sido ultrapassado na data de 17/5/2020 (IIQ: 12/5/2020 a 22/5/2020). Tal demanda, superior ao número de leitos públicos de UTI cadastrados, seria mantida por, ao menos, 125 dias (IIQ: 115 a 135).
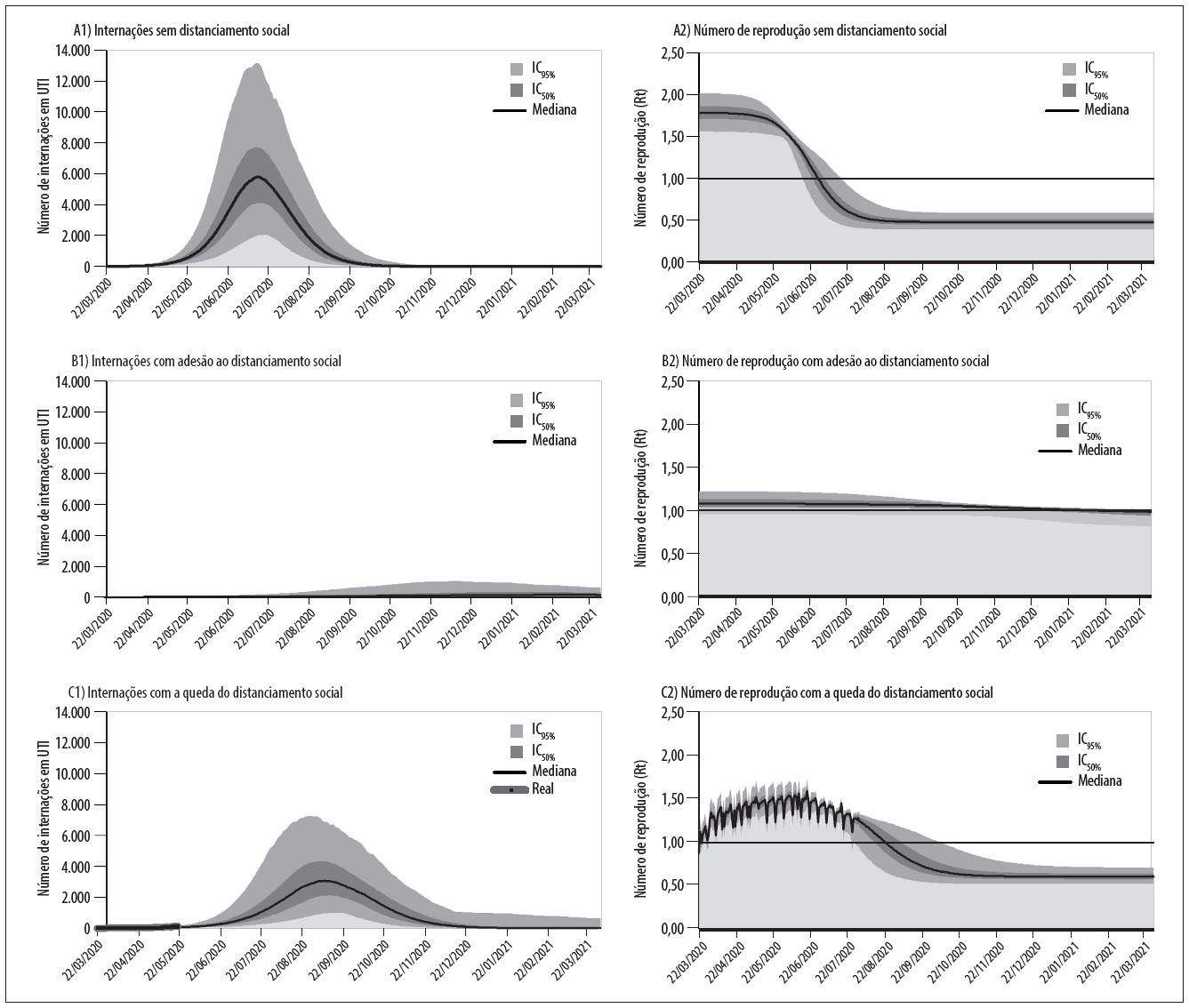
Figura 3 Projeções da demanda por leitos de UTI pela COVID-19 e do número de reprodução instantâneo (Rt) nos cenários (A) Perfil de propagação sem adesão às medidas de distanciamento social, (B) Perfil de propagação com manutenção da adesão ao distanciamento social e (C) Perfil de propagação com a dinâmica observada de queda do nível de distanciamento social, no Distrito Federal, Brasil
No horizonte de um ano, seria provável um pico de 178.615 infecções ativas (IIQ: 153.820 a 203.955) na data de 1/7/2020 (IIQ: 26/6/2020 a 6/7/2020). Nesse ritmo, até a data de 31/3 do próximo ano (2021), seria prevista a infecção de até 73,2% da população do Distrito Federal (IIQ: 70,3 a 75,9%). Mesmo que fosse possível atender a todos os infectados, seria prevista a morte de 16.143 indivíduos (IIQ: 10.948 a 22.326) - letalidade esperada de 0,67% (IQR: 0,45 a 0,94%).
Cenário B - Perfil de propagação com manutenção da adesão ao distanciamento social
Considerando-se a hipótese de que se mantivesse a adesão no nível de isolamento social médio de 57,38%, obtido no período inicial das medidas de distanciamento, este cenário previa um pico de 189 internações em UTI (IIQ: 57 a 394) somente na data de 7/3/2021 (IIQ: 6/1/2021 a 31/1/2021) e, nesse contexto, seria factível atender a demanda com o número de leitos cadastrados no Distrito Federal.
Ao longo do período simulado de um ano, o número total de indivíduos infectados poderia atingir um pico de 5.269 infecções ativas (IIQ: 1.538 a 11.549). Até a data de 31/3/2021, o total de infecções acumuladas alcançaria apenas 7,6% da população do Distrito Federal (IIQ: 3,0 a 16,4%) e, com uma letalidade de 0,70% (IIQ: 0,47 a 0,94%), seriam esperados até 1.438 óbitos (IIQ: 583 a 3.234).
Cenário C - Perfil de propagação com a dinâmica observada de queda do nível de distanciamento social
Seguindo a proposta metodológica descrita para este cenário, o coeficiente de transmissão acompanhou a variação dinâmica do nível de isolamento registrado até a data de 31/7/2020. A partir de 1/8/2020, considerou-se a manutenção do nível de isolamento médio de 39,7%, conforme os valores registrados nos últimos cinco dias disponíveis. 11 Com isso, projetou-se que a queda observada do nível de distanciamento propiciaria um pico de até 3.460 internações em UTI (IIQ: 2.634 a 4.779) na data provável de 10/9/2020 (IIQ: 31/8/2020 a 22/9/2020) ( Figura 3 ). Neste cenário, mesmo ao se elevar o nível de isolamento a uma média de 70% (valor próximo ao máximo obtido na data de 22/3/2020) a partir do dia 1/8/2020, ainda seria possível observar um pico de 2.097 internações (IIQ: 1.245 a 3.312) na data de 19/8/2020 (IIQ: 16/8/2020 a 21/8/2020). Entretanto, a interrupção completa do distanciamento, retornando-se ao nível de isolamento de 30% observado antes da implementação das políticas de distanciamento, poderia provocar uma demanda com um pico de 4.812 internações em UTI (IIQ: 3.643 a 6.283) em 12/9/2020 (IIQ: 04/9/2020 a 21/9/2020).
Discussão
A partir de indicadores e dados públicos utilizados nesta análise, é possível identificar a adesão ao distanciamento social após a publicação do primeiro decreto de medidas de enfrentamento à COVID-19 no Distrito Federal. Igualmente, relacionando-se a evolução temporal do nível de isolamento com a consequente redução progressiva da propagação da doença (Rt), seria possível alcançar valores de referência para o controle de surtos e, ao mesmo tempo, postergar e reduzir o pico de internações em UTI para uma estimativa plausível diante da capacidade da rede assistencial local.
Diferentemente do cenário de manutenção do distanciamento social, todos os cenários de ausência de distanciamento social, seja pela não implementação das medidas (Cenário A), seja pela baixa adesão (Cenário C), mostram uma previsão compatível com o colapso da rede local devido à alta demanda por internações em UTI. Não obstante a incerteza sobre a data e a magnitude da demanda, as projeções alternativas do Cenário C, que busca incorporar os percentuais observados de isolamento social, apontaram picos de internações em meados de agosto e setembro deste ano. Tais projeções são consistentes com a situação de espera por leitos de UTI no Distrito Federal relatada no mês de agosto. Também coerentes com os achados de análise recente sobre outros estados brasileiros, realizada por pesquisadores do Imperial College London, 22 não obstante reduções significativas da propagação de casos, os níveis de isolamento alcançados ainda perpetuariam um Rt >1, indicando a manutenção do crescimento epidêmico da COVID-19 no Distrito Federal.
Apesar de esta análise ser restrita ao contexto do Distrito Federal, ela mostra a magnitude do efeito potencial do distanciamento sobre a necessidade de leitos, sendo improvável que tal relação, mesmo em magnitude diferente, não se generalize para outros contextos. Os resultados são também consistentes com outras iniciativas de análise do distanciamento social, 4 incluindo contextos nacionais, como a análise dos efeitos positivos do distanciamento social e da redução de fluxo intermunicipal no controle da COVID-19 na Bahia, pela Rede CoVida, 6 cujos dados disponíveis sugerem, fortemente, que as medidas tomadas conseguiram suavizar a curva da epidemia naquele estado.
O modelo aqui adotado segue as linhas metodológicas compatíveis com a dinâmica populacional de infecções 13 e foi construído sobre parâmetros locais, na medida do possível, incluindo o ajuste da taxa de infecção e letalidade para a estrutura etária do Distrito Federal. Ademais, buscou-se o uso transparente das evidências disponíveis e a condução robusta das incertezas paramétricas, mediante simulações de Monte Carlo. 20 Conforme demonstrado nesta análise, o acompanhamento de indicadores dinâmicos de isolamento e propagação da infecção, como a estimativa do Rt, acompanhados de sua incerteza, apresenta-se como uma estratégia eficiente e pragmática de monitoramento das políticas de enfrentamento da COVID-19. 23
Apesar de os modelos compartimentais em nível de valor esperado conseguirem representar o comportamento médio de epidemias nas populações, eles não são capazes de retratar histórias individuais. 12 Da mesma forma, a estimativa dos valores dinâmicos das taxas de contatos efetivos é discutida em abordagens variadas, na literatura, com diferentes impactos potenciais nos resultados, de acordo com o método de cálculo. 24 Embora considerados os ajustes relativos à estrutura etária local e calibração com base nos registros de internações disponíveis, não foram considerados outros fatores capazes de interferir nos cenários de projeção, a exemplo das comorbidades relacionadas à maior gravidade da progressão da doença, incluídas doenças cardiovasculares, respiratórias e endócrinas. 25 E ainda sobre as características demográficas e sociais, ressalta-se que o modelo assume a premissa de contato aleatório, e os valores de suas estimativas podem divergir das médias obtidas quando considerados os padrões específicos de contato de cada grupo (influência da heterogeneidade). Ao se interpretar o número de mortes esperadas no modelo, é importante lembrar: não foi considerada a possibilidade de aumento de mortes por falta de leitos em um possível colapso da rede assistencial.
Por fim, ressalta-se que os dados de leitos cadastrados, aqui apresentados, também devem ser interpretados com atenção à referência das metas de redução do impacto sobre a rede hospitalar. Isto porque não consideram as proporções reais de ocupação por outras condições clínicas, e os leitos adicionais que já vêm sendo implementados pelas autoridades de saúde.
A despeito de suas limitações, a presente análise reforça as conclusões sobre o efeito positivo das medidas de distanciamento social na redução do impacto da propagação da COVID-19 sobre a demanda da rede hospitalar. Dado o cenário alarmante projetado com a interrupção ou baixa adesão ao distanciamento social, é essencial que as autoridades em saúde locais considerem o monitoramento diário de indicadores de distanciamento, disseminação da doença e disponibilidade de leitos hospitalares, no planejamento e implementação das políticas públicas de enfrentamento à COVID-19.










 texto em
texto em