The principle of parsimony recommends: when faced with simple or complex solutions, the simplest solution is always the first choice,1 since “it is vain to do with more what can be done with fewer.”2 This principle is also known as “Ockham's razor”, a concept derived from philosophy, which has gradually been incorporated by other fields of knowledge - including epidemiology, where it has proven useful in the analysis of time series.3
From this perspective, simple explanations are to be preferred for times series, this being a characteristic found in the definition given by Hyndman and Athanasopoulos,4 for whom a time series is a list of numbers accompanied by information regarding the time when they were recorded. It is a series because it is a list, that is, a sequence, usually uninterrupted, of numbers; and it is temporal because it necessarily requires data about the time when the dependent variable under study was collected. It follows that any discussion of time series emphasizes time, taken as a variable.
Paradoxically, it is usual to conceive of time not as a variable but as a series. As such, time is a succession of instants and each instant, considered as the smallest discernible space of time itself, contributes to forming an uninterrupted and eternal series. Time, as an uninterrupted and endless series of instants, is a physical phenomenon. It is, however, also a cultural phenomenon, which attracts the interest of everyone, including the interest of Einstein and Dalí. In his famous 1931 painting The Persistence of Memory, which has been on display at the Museum of Modern Art in New York since 1934,5 surrealist Salvador Dalí expresses pictorially the fleetingness of time as a series of instants, through remarkable melted clocks. Dalí’s composition seeks to apprehend, in oil paint on canvas, human perception regarding this physical greatness. Curiously, this painting, which eternalizes in aesthetic creation a perception of time, is itself, in its materiality, an expression of time. Whoever looks at the painting may well wonder how long it took the author to conceive and execute it. Dalí’s account is that it all happened in a short space of two hours.6
Notwithstanding, The Persistence of Memory is not only concerned with time, but also with something intrinsically related to it. Dalí provides the clue when enunciating the name of the painting: it is also concerned with memory. Conceiving and executing the painting may have taken less than two hours, and this would not be possible without its author’s memory. Whoever observes The Persistence of Memory beyond the iconic melting clocks, visualizes, in the foreground of the canvas, the trunk and a branch of an olive tree. Olive trees are common in Catalonia, Dalí’s homeland, the landscapes of which appear in several of his paintings. The landscape in the background of The Persistence of Memory is that of Port Lligat in 1931, now a seaside village and home to the painter’s home-museum in the Spanish town of Cadaqués, the destination of many of his childhood vacation trips and the place where he was introduced to modern art.5,6
Memory operates with recollections, with the ability to preserve not only images, as seen in Dalí’s paintings, but impressions, knowledge and experiences acquired in the past. Memory is, therefore, a way of marking time. In Dalí’s most famous work, the clock, an object-symbol of time, melts when exposed to The Persistence of Memory.7 It is as if the series of instants, uninterrupted and eternal, changed its form with the modification of each instant that constitutes it, making it difficult for the series to discern the recording of each one of these smaller spaces of time itself. This therefore also makes the task of those who intend to analyze it more difficult.
The purpose of this digression on Dalí’s classic work and emphasis on time series analysis refers to time, as well as memory. It is as if studies of phenomena measured on a monthly basis, for example, consider that data referring to a given month has memory, that is, as if it “remembers” what happened in the immediately preceding month. What happens at one point in time is not something isolated but rather is strongly influenced by what happened at previous points. This idea is simple to understand. Yesterday’s trading dollar rate gives a good idea of today’s rate. The previous year’s infant mortality rate in a country is a very reasonable approximation of the value of this indicator in the current year. However, this memory is not always restricted to the immediately preceding record. If the phenomenon under study has seasonal variation, this memory may extend to the months that follow.
Therefore, if time series data somehow have memory, this must be dealt with. Shumway and Stoffer8 state that the fact that the value of the series at time t (referred to here as Yt) depends on past values (Yt-1, Yt-2 and so forth), gives rises to sui generis problems in statistical modelling and inference. This correlation between the values of the series - called autocorrelation, since it measures the linear relationship between the variable Y and itself in a previous period - greatly restricts the applicability of conventional statistical methods, such as linear regression, which has randomness and independence of the residuals as one of its underlying assumptions.8 It is in this space that time series analysis is situated, and is justified, since it answers the mathematical and statistical questions arising from these correlations.
This dependence on past values gradually reduces in the case of times further away from time t, which means that the autocorrelation coefficients are larger at points closer to t and smaller at more distant points. The calculation of the correlation coefficient of the series at time Yt with itself, that is, with the series at time Yt, evidently results in 1, and is called lag 0 autocorrelation. The same calculation of the series at time Yt with the series at time Yt-1 corresponds to the lag 1 autocorrelation, that is, the first autocorrelation. It can therefore be deduced that the lag 2 autocorrelation is obtained by computing the correlation of Yt with Yt-2, and so on. The autocorrelation coefficients are commonly plotted on a graph called an “autocorrelation function”. When there is seasonality, for example, the autocorrelations are larger for the lags corresponding to the seasonal variations than for the others.4
Given the insufficiency of classical regression in explaining the dynamics of a time series, it is necessary to use procedures that address the problem of serial autocorrelation of residuals. The Prais-Winsten method, first described in 1954,9 is an alternative for trend estimation, commonly adopted in epidemiological studies. This method is equivalent to a first-order autoregressive model, since it performs autocorrelation correction of the first-order residuals, that is, lag 1, and not of larger lags. This method does not therefor account for all possible lags. In general, first-order residual autocorrelation correction contributes to correction in other lags; sometimes, however, it does not. It is important to pay due attention to this detail so as to avoid inadequacies or errors.
The use of Prais-Winsten regression models in epidemiological studies to verify the existence of trends, including for seasonal data, was described in an article published in Epidemiology and Health Services - journal of the Brazilian National Health System (Epidemiologia e Serviços de Saúde: revista do SUS - RESS) in 2015.10 A review of articles published in the RESS in 2014, the year in which the journal was indexed in the SciELO collection,11 up to the third issue published in 2022, reveals the use of this method in 35 studies which aimed to estimate the trend of a variety of phenomena, ranging from homicides to cancer, and from COVID-19 to the granting of welfare benefits. In just one issue of RESS volume 31, published in 2022, five papers were identified that made use of the Prais-Winsten procedure. There was no record of an article adopting this method in 2014.
The article published in the RESS potentially influenced epidemiological studies presented in other journals. Between 2015 and 2022, 153 articles were published that used this method to assess the trend of health indicators in Brazil. In addition to the 35 published in the RESS, 20 were published in the Revista de Saúde Pública, 13 in the Cadernos de Saúde Pública, 12 in the Ciência & Saúde Coletiva, five in the Revista Brasileira de Epidemiologia and 68 in other journals, including journals published abroad and with wide international circulation. The articles refer to mortality and incidence rates of different diseases and health conditions, as well as indicators of health service provision and performance (Figure 1).
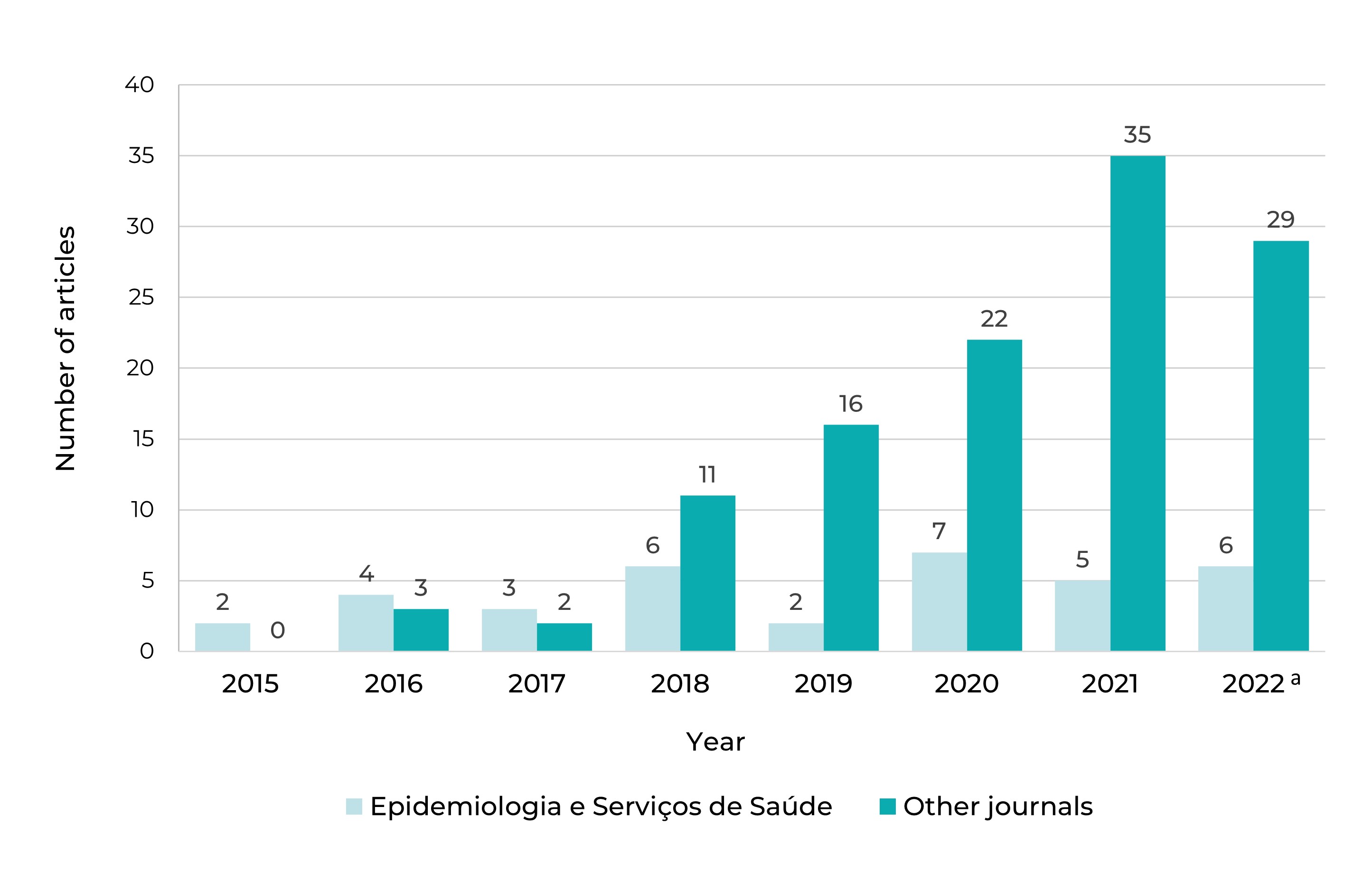
a) Until october/2022
Figure 1 Number of articles that used the Prais-Winsten method to assess health indicators in Brazil, published 2015-2022
In 2022, RESS is celebrated its 30th anniversary. Anniversaries are markers of time and memory, the two nouns that inspired Dalí, and that grow in the same direction: successive increases in one determine increases in the other. It is in this sense that the RESS’ desire emerges to continue contributing to the consolidation of the memory of the epidemiological knowledge produced in health services. And may the RESS continue to be a reference for the workers of the Brazilian National Health System (Sistema Único de Saúde).










 texto em
texto em 
 Curriculum ScienTI
Curriculum ScienTI