O princípio da parcimônia preconiza: frente a soluções simples ou complexas, a primeira opção recai sempre no simples,¹ pois “é inútil fazer com mais aquilo que pode ser feito com menos”.² Este princípio é também conhecido como a “navalha de Ockham”, um conceito oriundo da filosofia, que vem sendo paulatinamente apropriado por outros campos do conhecimento - inclusive a epidemiologia, área em que se tem mostrado útil à análise de séries temporais.³

Nessa perspectiva, deve-se dar preferência a explicações simples, característica em que se insere a definição de Hyndman e Athanasopoulos,⁴ para quem uma série temporal é uma lista de números acompanhada de informações relativas ao tempo no qual foram registrados. É uma série porque é uma lista, ou seja, uma sequência, geralmente ininterrupta, de números; e é temporal, pois requer, necessariamente, dados sobre o tempo em que determinada variável dependente sob estudo foi coletada. Deduz-se que qualquer discussão sobre série temporal coloca sob ênfase o tempo, tomado como uma variável.

Paradoxalmente, é usual conceber o tempo não como uma variável, e sim como uma série. O tempo seria uma sucessão de instantes e cada instante, tido como o menor espaço discernível do próprio tempo, estaria a compor uma série ininterrupta e eterna. O tempo, enquanto uma série ininterrupta e sem fim de instantes, é um fenômeno físico, mas também cultural, a atrair para si o interesse de muitos, inclusive de Einstein e Dalí. Na célebre tela A persistência da memória, pintada em 1931 e exposta no Museu de Arte Moderna de Nova York desde 1934,⁵ o surrealista Salvador Dalí expressa, pictoricamente, a fugacidade do tempo como série de instantes, por meio dos notabilíssimos relógios derretidos. A composição de Dalí busca apreender, em tinta a óleo sobre tela, a percepção humana a respeito dessa grandeza física. Curiosamente, essa tela, que eterniza em criação estética uma percepção do tempo, é, ela própria, em sua materialidade, expressão do tempo. Frente à obra, qualquer pessoa se interroga sobre quanto tempo o autor teria levado para concebê-la e executá-la. Dalí conta que tudo aconteceu em um intervalo de duas horas.⁶

Não obstante, A persistência da memória não se ocupa apenas do tempo, mas de algo intrinsecamente relacionado a ele. Dalí dá a pista ao enunciar o nome da tela: a obra se ocupa também da memória. Conceber e executar a tela pode ter tido a duração de menos de duas horas, e isso não seria possível sem a memória do autor. Quem observa A persistência da memória para além dos icônicos relógios a derreter, visualiza, no primeiro plano da tela, o tronco e um galho de oliveira. A árvore é comum na Catalunha, terra natal de Dalí, cujas paisagens aparecem em várias de suas pinturas. A vista ao fundo é a de Port Lligat em 1931, hoje uma vila à beira-mar e que abriga a casa-museu do pintor, na cidade espanhola de Cadaqués, destino de muitas de suas viagens de férias na infância e local de onde foi apresentado à arte moderna.^5,6

A memória opera com lembranças, com a capacidade de preservar não apenas imagens, conforme se vê nas pinturas de Dalí, senão impressões, conhecimentos e experiências adquiridos no passado. A memória é, portanto, uma forma de marcar o tempo. Na obra mais famosa de Dalí, o relógio, objeto-símbolo do tempo, derrete ao ser exposto à persistência da memória.⁷ É como se a série de instantes, ininterrupta e eterna, mudasse sua forma a partir da modificação de cada instante que a constitui, conferindo à série dificuldades para discernir o registro de cada um desses menores espaços do próprio tempo. E assim, tornando mais difícil a tarefa de quem se propõe a analisá-la.

O propósito dessa digressão sobre a obra clássica de Dalí e a ênfase na análise de séries temporais refere-se ao tempo, como também à memória. Estudos de fenômenos aferidos, por exemplo, mensalmente, consideram como se o dado referente a um determinado mês tivesse memória, ou seja, que se “lembrasse” do ocorrido no mês imediatamente anterior. O que acontece em um ponto no tempo não é algo isolado, mas fortemente influenciado pelo que se passou nos pontos precedentes. Essa ideia é de simples compreensão. A cotação do dólar comercial de ontem fornece uma boa ideia da cotação de hoje. O coeficiente de mortalidade infantil de um país no ano passado é uma aproximação, bastante razoável, do valor desse indicador no presente ano. Contudo, nem sempre essa memória fica restrita ao registro imediatamente anterior. Se o fenômeno estudado tem variação sazonal, essa memória pode se estender aos meses seguintes.

Logo, se os dados de séries temporais possuem, de algum modo, memória, é preciso lidar com isso. Shumway e Stoffer⁸ afirmam que o fato de o valor da série no tempo t (denominado aqui de Yt) depender dos valores passados (Yt-1, Yt-2 e daí por diante) origina problemas sui generis na modelagem e inferência estatística. Essa correlação entre os valores da série - denominada autocorrelação, uma vez que mede a relação linear entre a variável Y e ela mesma em um período anterior - restringe sobremaneira a aplicabilidade de métodos estatísticos convencionais, como a regressão linear, que tem na aleatoriedade e independência dos resíduos um de seus pressupostos.⁸ É nesse espaço que a análise de séries temporais se situa, e se justifica, posto que responde às questões matemáticas e estatísticas emergentes dessas correlações.

Essa dependência quanto aos valores passados reduz-se gradativamente, para tempos mais afastados do tempo t, o que significa dizer que os coeficientes de autocorrelação são maiores nos pontos mais próximos de t e menores nos mais distantes. O cálculo do coeficiente de correlação da série no tempo Yt consigo mesma, isto é, com a série no tempo Yt, evidentemente resulta em 1, sendo denominada de autocorrelação de lag 0. O mesmo cálculo da série no tempo Yt com a série no tempo Yt-1 corresponde à autocorrelação de lag 1, ou seja, primeira autocorrelação. Deduz-se, então, que a autocorrelação de lag 2 é obtida calculando-se a correlação de Yt com Yt-2, e daí por diante. Os coeficientes de autocorrelação são comumente plotados em um gráfico denominado “função de autocorrelação”. Quando há sazonalidade, por exemplo, as autocorrelações são maiores para os lags correspondentes às variações sazonais do que para os demais.⁴

Dada a insuficiência da regressão clássica na explicação da dinâmica de uma série temporal, é preciso utilizar procedimentos que deem conta do problema da autocorrelação serial dos resíduos. O método de Prais-Winsten, descrito primeiramente em 1954,⁹ é uma alternativa para estimação de tendência, comumente adotada em estudos epidemiológicos. Esse método equivale a um modelo autoregressivo de ordem 1, pois efetua correção de autocorrelação dos resíduos de primeira ordem, ou seja, de lag 1, e não de defasagens maiores. Dessa forma, o método não contempla todas as defasagens possíveis. Em geral, a correção da autocorrelação dos resíduos de primeira ordem contribui para a correção em outras defasagens; às vezes, porém, não. É importante dar a esse detalhe a devida atenção, para não incorrer em impropriedades ou erros.

O uso de modelos de regressão de Prais-Winsten em estudos epidemiológicos para verificação da existência de tendência, inclusive para dados sazonais, foi descrito em artigo publicado na Epidemiologia e Serviços de Saúde: revista do SUS (RESS) em 2015.¹⁰ Uma revisão de artigos publicados na RESS em 2014, ano de indexação da revista na coleção SciELO,¹¹ até o terceiro número publicado em 2022, revela o uso desse método em 35 estudos que objetivaram estimar a tendência de fenômenos variados, de homicídios a câncer, passando por covid-19 e concessão de benefícios previdenciários. Em um único número do volume 31 da RESS, publicado em 2022, foram identificados cinco trabalhos que fizeram uso do procedimento de Prais-Winsten. Não houve registro de artigo que tenha adotado esse método em 2014.

O artigo publicado na RESS potencialmente influenciou estudos epidemiológicos apresentados em outros periódicos. Entre 2015 e 2022, foram publicados 153 artigos que se utilizaram desse método para avaliar a tendência de indicadores de saúde no Brasil. Além dos 35 publicados na RESS, houve 20 na Revista de Saúde Pública, 13 nos Cadernos de Saúde Pública, 12 na Ciência & Saúde Coletiva, cinco na Revista Brasileira de Epidemiologia e 68 em outras revistas, inclusive periódicos editados no exterior e de grande veiculação internacional. Os artigos referem-se a coeficientes de mortalidade e incidência de diferentes doenças e condições de saúde, bem como indicadores de provisão e desempenho dos serviços de saúde (Figura 1).

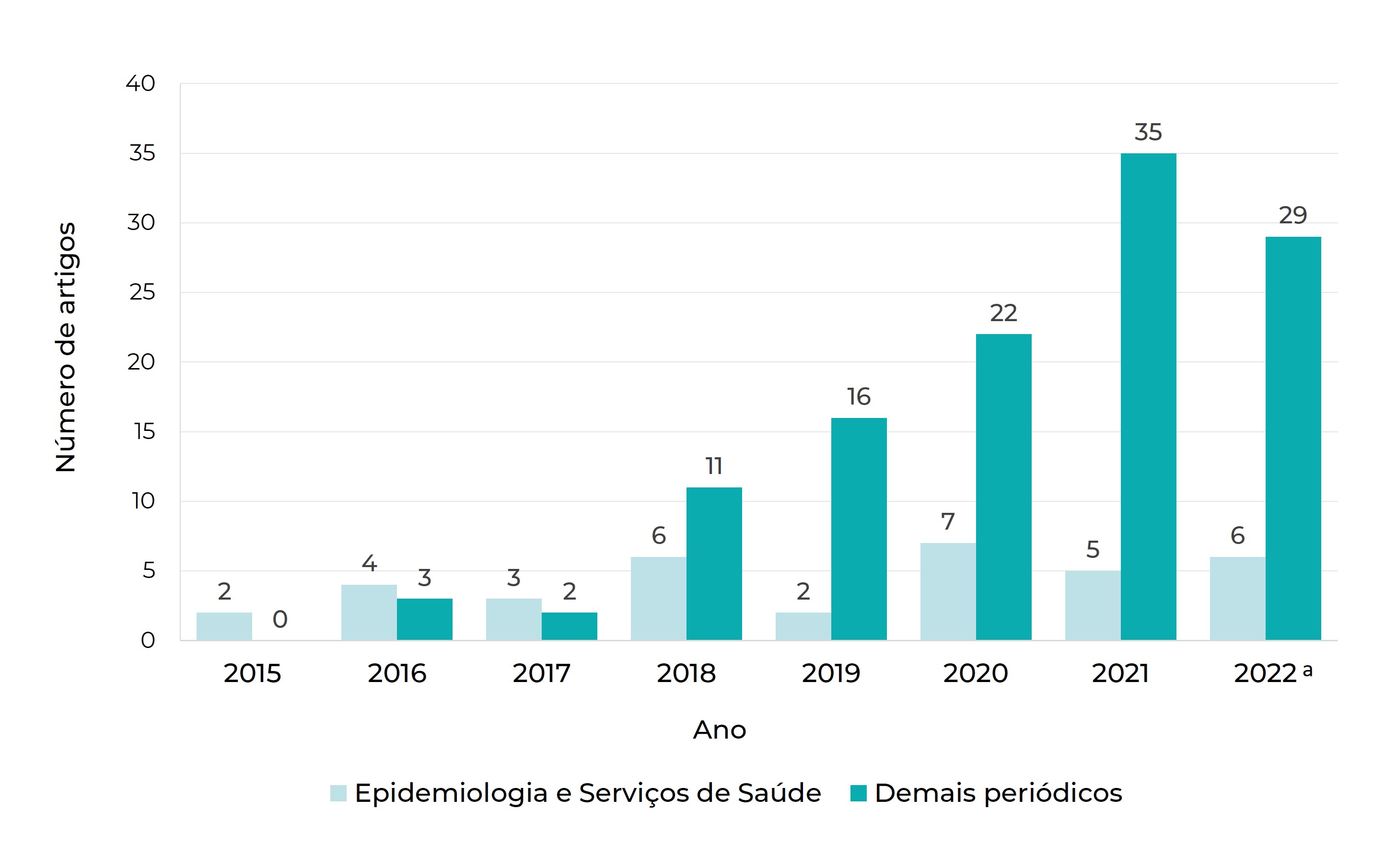
a) Até outubro/2022.

Figura 1 Número de artigos que utilizaram o método de Prais-Winsten para avaliar indicadores de saúde no Brasil, publicados em 2015-2022 

Em 2022, a RESS celebra 30 anos de existência. Aniversários são marcadores do tempo e da memória, os dois substantivos inspiradores de Dalí, e que crescem no mesmo sentido: aumentos sucessivos e um determina acréscimos no outro. É nesse sentido que emerge o desejo de a RESS permanecer contribuindo para a consolidação da memória do conhecimento epidemiológico produzido nos serviços de saúde. E que a revista siga sendo uma referência para os trabalhadores do Sistema Único de Saúde.